Stiffness characteristic comparison between metal-rubber and rubber isolator under sonic vibration

Yu, Wang; Zhijun, Li; Baolin, Liu; Mingshuai, Gao

Journal of Vibroengineering

Browse Journal

Submit article

Published: 31 March 2014

Check for updates

Stiffness characteristic comparison between metal-rubber and rubber isolator under sonic vibration

Wang Yu¹

Li Zhijun²

Liu Baolin³

Gao Mingshuai⁴

^{1, 2, 3, 4}Key Laboratory on Deep Geo-Drilling Technology of the Ministry of Land and Resources China University of Geosciences, Beijing 100083, P. R. China

Corresponding Author:

Wang Yu

Cite the article Download PDF

Downloads 1770

Abstract

Stiffness of rubber and metal rubber (MR) changes nonlinearly. Based on hysteretic damping theory and energy conservation equations, a unified stiffness model is developed. The ring type of isolators made from rubber and metal rubber are studied. The isolator samples are tested on the electro-hydraulic loading system, which is fixed by a clamping device. We aim to study the deformations under different loading rates, loading forces and other quasi-static loading states. The dynamic stiffness affected by the preload and vibration frequency is studied on the sonic drilling processing. It can be concluded that the metal rubber isolators deform larger plastic than the rubber. The damping, plastic deformation and elastic deformation of the metal rubber and rubber material are inversely proportional to the loading rate. The total deformation of the rubber is larger than the metal rubber, no matter when the load increases or decreases. The dynamic stiffness of the metal rubber isolator is proportional to the vibration frequency. However, the dynamic stiffness of the rubber remains the same under different preloads, while decreases when the preload increases.

1. Introduction

Rubber is a kind of viscoelastic material, and it has a large loss factor [1] which isolates vibration effectively, but it does not apply to corrosion and high temperature [2]. Metal rubber, also called wire mesh dampers [3-5], consists of many wire helixes which consume vibration energy by relative slip friction. The dry friction damping theory [6-9] is used to study the microstructure of metal rubber, while the viscoelastic characteristics are its main feature in the macrostructure study [10-12] and some research has been accomplished [3-16]. Some models such as small curved beam [9], the theory of energy equality [17-18], and finite element model [19] are utilized to study the stiffness characteristics of metal rubber. Complex stiffness method is commonly used for damping and loss factor to determine rubber resilient elements to gain further characterize [20-22]. He et al [23] studied viscoelastic hollow rubber cylinders using the exact three-dimensional theory. By determining the stiffness and phase angle for different preload conditions and force amplitudes, which use wattmetric method and discrete Fourier transformation for increasing reliability of the data Mu, Jia and Ladislav P applied semi-analytical finite elements to study propagating modes in hollow cylindrical pipes, which is used to study the rubber element for reduction of vibration from railway wheels. [24-26]. In order to give better estimation of the stress response, Ciambella et al. developed a non-linear viscoelastic constitutive model of rubber to obtain material parameters [27]. Radial stiffness of finite length of rubber tube is reconstructed based on the Fourier-Bessel functions by Hill [28], while its numerical calculation is very complicated [29]. Horton [30, 31] optimized the rubber tube by the variant Bessel functions. Other articles [19, 32, 33] study the stiffness model by the test date, but there are no any other studies comparing the stiffness characteristics between the rubber and metal rubber under sonic vibration status whose vibration frequency is 5-200 Hz with heavy cyclic load. It is significantly important to compare these two kinds of material when the isolators as select to design the vibration equipments.

To select a proper isolator for the vibration equipment, the unified model of the rubber and metal rubber are developed. The annular isolators made from rubber and metal rubber are designed and manufactured with the same structure. The clamp mechanism and inertial exciter are also manufactured to test the stiffness under the static and dynamic loading state. We studied the influence of different loading rates, loading force on the axial deformation of the isolator in quasi-static. Additionally, we researched the dynamic stiffness affected by the preload and vibration frequency.

2. Model of two kinds of material isolator

2.1. Isolator linear micro-modulus

The metal rubber isolators (Fig. 1(a)) are made of a ∅0.18 mm wire consisting of 1Cr18Ni9Ti. The spiral is bent from the wire and it can be pressed into an annular isolator in the mold [30-31]. The relative density of metal rubber isolator sample is 0.6. The outer diameter and inter diameter are 70 mm and 34 mm respectively. Its height is 23 mm. With same structure with the mental rubbers, the rubber isolators (Fig. 1(b)) are manufactured by drilling and its density is 0.127 kg/m³.

Fig. 1Metal rubber isolator and rubber isolator

a) Metal rubber isolator

b) Rubber isolator

Metal rubber and rubber are both porous. Suppose that the isolator is divided into tiny cubic unit characterized by continuous media and anisotropy as Fig. 2. Its bending deflection dominates the axial and shear defection.

Fig. 2Three-dimensional structure of isolator and its deformation

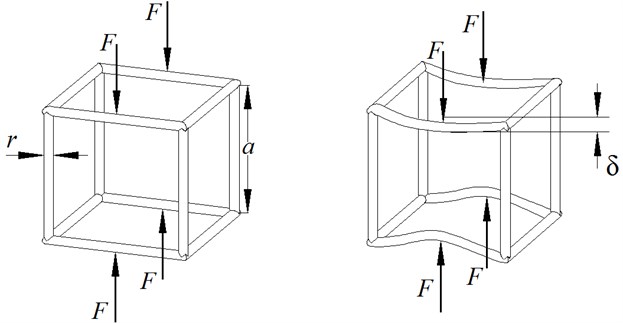
Suppose that $a$ is the side length and $r$ is the radius of beam. When the force $F$ is exerted at the middle of the beam without lateral bending, the maximum deflection of clamped-clamped beam can be expressed as Eq. (1):

1

\{\begin{array}{l} δ = \frac{F a^{3}}{48 E I}, \\ F = σ a^{2}, \\ I = \frac{π r^{2}}{4}, \end{array}

where $E$ represents elastic modulus, $I$ is sectional inertia moment for beam, $σ$ is stress of the beam.

Bases on the assumption that each unit has equal mass, the relationship between the two kinds of mass calculation method can be expressed as Eq. (2):

2

ρ a^{3} n = 12 ρ_{i} π {x r}^{2} a n,

where $ρ$ is the isolator density, $ρ_{i}$ is the imaginary density of the tiny cubic unit side (to metal rubber is the density of metal material ), and $n$ is the number of the tiny cubic unit.

The stress-strain of the isolator under compression force can be refered to Eq. (3):

3

\{\begin{array}{l} ε = 2 \frac{δ}{a}, \\ σ = \frac{F}{S}, \\ ε = \frac{X}{a}, \end{array}

where $ε$ is the strain of the isolator, $S$ represents the compression area, and $X$ is the original thickness change of ithe isolator.

When considering Eq. (1)-(3), $K$ is the shape factor, the approximate linearization formula between stress and strain for the microstructure can be linearly expressed as Eq. (4):

4

F = (\frac{E S ρ^{2}}{24 π ρ_{i} a}) ∙ X = K ∙ X .

The results above show that the stiffness is proportional to elastic modulus, forced area, and isolator density but inversely to metal density and unit length. A less unit length will lead to a better stiffness. Rubber performs better than metal rubber in terms of uniformity. When compressed, the dry sliding friction will be generated between the tiny cubic units, and the stiffness changes nonlinearly due to distinct parameters.

2.2. Isolator nonlinear micro-modulus

Both rubber isolator and metal rubber isolator have a symmetry hysteresis [28]. When the isolator undergoes a load outside, the restoring force $(F)$ will be generated. There are two parts of it: one is the elastic force $(F_{k})$ linear with the deformation of isolator $(x)$ , the other is the damping force ( $F_{c}$ ), related to vibration amplitude ( $A$ ), loading rate, loading frequency ( $ω$ ), deformation [34] and shape factor ( $K$ ). It is specifically described as follows:

5

F = F_{k} (x, \dot{x,} K, A, ω) + F_{c} (x, \dot{x,} K, A, ω) .

The deformation of isolator affects the elastic force most. However, the damping force of the isolator ( $\dot{x}$ ), the vibration rate affects most. Elastic force and damping force are expanded on the basis of the deformation of isolator and the vibration rate of isolator ( $\dot{x}$ ). In terms of the mutual coupling between these factors, the secondary causes are ignored. As a result, elastic force and damping force can be expressed separately as follows:

6

\{\begin{array}{l} F_{k} (x, \dot{x,} K, A, ω) = \sum_{i = 1}^{(j + 1) / 2} K_{2 i - 1} (K, A, ω) ∙ x^{(2 i - 1)}, \\ F_{c} (x, \dot{x,} K, A, ω) = \sum_{i = 1}^{(j + 1) / 2} C_{2 i - 1} (K, A, ω) ∙ | {\dot{x} |}^{(2 i - 1)}, \end{array}

where $K_{2 i - 1} (K, A, ω)$ is the coefficient of stiffness, $C_{2 i - 1} (K, A, ω)$ is the coefficient of damping, and $j$ is the cardinal number which can decide the fitting accuracy.

Expand the above equation to the second classes, so the total stifness coefficient ( $K^{*}$ ) is calculated as Eq. (7):

7

K^{*} = \frac{K_{1} (K, A, ω) ∙ x + K_{2} (K, A, ω) ∙ x^{2} + C_{1} (K, A, ω) ∙ \dot{| x} | + C_{1} (K, A, ω) ∙ | {\dot{x} |}^{2}}{x} .

When absorbing energy from the external load, the shape of isolator will be changed. The energy theory is performed in two ways. One part is absorbed in a way of elastic deformation and then transformed into potential energy [35]. The other part is consumed by the inner sliding friction of the wire in isolator and transformed into heat [36]. Based on the principle of the virtual work, the energy of the external load ( $W$ ) is equal to the sum of the heat consumed by damping energy ( $C)$ and deformation energy ( $U$ ). The formula is as follows:

8

U + C = W .

The shearing modulus of elasticity is ignored under axial loading, while the modulus of elasticity mainly undergoes tension and compression. The deformation energy of the isolator is as follows:

9

U = \int_{0}^{l} \frac{M^{2} (s)}{2 E^{'} ∙ I^{'}} d s,

where $M (s)$ is the moment of the isolator under axial loading, and $I^{'}$ is the inertia of the annulus isolator. $E^{'}$ is the modulus of elasticity which is relaxed with the material of isolator, including the modulus of rubber ( $E_{x}$ ) and the modulus of metal rubber ( $E_{j}$ ). The modulus of metal rubber is determined by modulus of metal wire ( $E$ ), diameter of metal wire ( $d$ ), pitch of the spiral ( $h$ ), diameter of spiral ( $d_{h}$ ) [6]. Formula of modulus of metal rubber is as follows:

10

E_{j} = \frac{3 E h d^{4}}{8 d_{h}^{5}} .

Two force sensors are installed at the top and the bottom of the isolator to measure the damping force. The pressure difference of the two force sensors is equal to the damping force ( $f_{c}$ ). The damping energy can be calculated as the product of the damping force and axial deformation:

11

C = f_{c} ∙ x .

The value measured by the top sensor is the restoring force ( $F$ ). The energy of the external load can be calculated as the restoring force and axial deformation without any radial deformation (Eq. (12)):

12

W = \frac{1}{2} ∙ F ∙ x .

The Eq. (1)-(12) are models of the stiffness of the isolators. The damping force and the elastic force can be fitted by the test data.

3. Quasi-loading test

3.1. Quasi-static loading test plant

The change of dynamic stiffness is nonlinear, and it is related to many factors [37]. To study the stiffness, rock tri-axial test plant (TAW-2000) is used to conduct the axial quasi-static loading experiment of the annulus isolator characteristics (Fig. 3). A clamping device fixed on the annulus isolator is designed.

Fig. 3Experiment principle schematic. 1 – loading cylinder, 2 – displacement sensor, 3 – force sensor, 4 – clamping device, 5 – annulus isolator, 6 – base

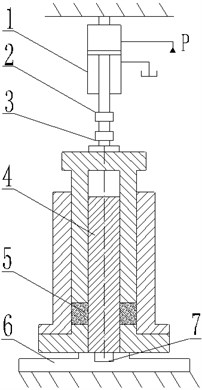
The isolator is fixed inside the clamping device (4). It is composed of piston, core rod and cylinder with high stiffness [38]. The axial force excited by the rock tri-axial test plant impacts the piston and the isolator. Two force sensors (3, 7) are installed to measure the loading and isolation force. The deformation of isolator is measured by the displacement sensor (2). The loading force can be adjusted by hydraulic pressure. However, the loading rate is subject to the flow of hydraulic oil in loading cylinder (1). A relief valve is set on the hydraulic circuit to prevent from abnormally high hydraulic pressure.

In order to study the stiffness under different loading rates and loading forces, the two loading stages include loading and unloading. When the loading conditions are the same, the differences between the rubber isolator and metal isolator are found by platform test.

3.2. Quasi-static loading test

3.2.1. Point loading test

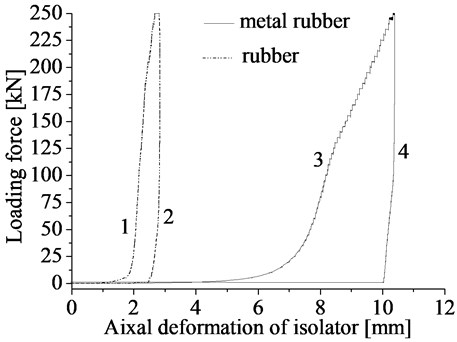
In order to eliminate hysteretic effect, the point loading test is performed in the isolator. The maximum loading force is 250 kN ± 5 kN.

Fig. 4 plots the isolator deformations under the point loading (1and 3) and unloading (2 and 4). Under the equal loading, the deformation of the metal rubber is larger. When the load disappears, the plastic deformation of metal rubber is 4.2 mm, compared with zero of the rubber.

Fig. 4Deformation of isolator under point loading test

3.2.2. Continuous loading test

Continuous loading test can reflect the hysteretic effect on the isolator material. The stiffness under different loading rates is tested at different loading times. Fig. 5 displays the isolator deformations under the different continuous loading rates. The curves (1) and (2) in Fig. 5 are the axial deformations of the metal rubbers with the loading rates of 12.5 kN/min and 25 KN/min. separately.

Fig. 5Deformation of metal rubber and rubber under continuous loading

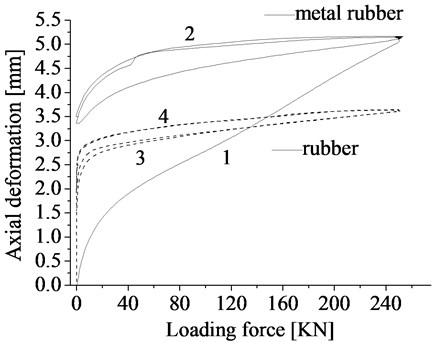
Fig. 5 presents the rubber. The result shows that the deformation of the metal rubber is bigger than the rubber. In terms of the loading rate, it is inverse proportional to the deformation of metal rubber. However, it has no relation to the rubber.

3.3. Dynamic characteristic test

Sonic drilling is driven by vibration (5-200 Hz) transmitted from the top driver by two balance rollers [39-40], which ensures the vibrations transmitted vertically down to the bit. By matching the natural resonance of the drill string, the frequency reaches a maximum penetration rate (Fig. 6(a)). In terms of the string, it is vibrated by a hydraulic drill head at an adjustable frequency [41, 42]. The oscillator is equipped with two eccentric counter-rotating balance weights, or rollers, which are timed to direct full vibration at 0º and 180º. However, a damper and a spring system in the top driver isolate vibration from the rest of the machine [43]. In order to test and verify the vibration isolation effect, (Fig. 6(b)), four accelerometers were attached to the housings of the two counter-rotating unbalanced rotors. Two others were attached to a part of the machine isolated from the drilling effect. Average acceleration value data was collected to calculate the excitation force and attenuated vibration force.

Fig. 6Model and test sketch of sonic vibration drilling

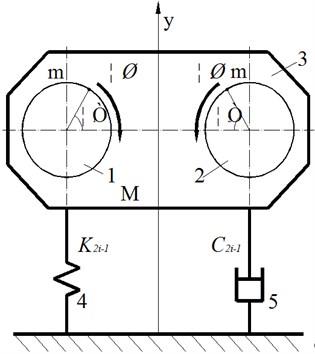
a) Model of sonic drilling

b) Field test

The sonic vibration frequency ranges from 5 to 200 Hz and isolator deformation ranges from 0 to 6 mm. The frequencies of 20, 100 and 200 Hz were selected as the frequency points when the preload is 3 KN. These three frequencies simulate the isolation characteristics of start-up, typical operating point and limit work status respectively. The vibration force changing with the displacement of the rubber isolator and metal rubber isolator are shown in Fig. 7. It shows that with the increase of the vibration frequency, the area enclosed by the hysteresis curve of the rubber and the metal rubber isolators increase dramatically. The curve areas of rubber are generally less than the metal rubber. It indicates that the damping force of the rubber is smaller.

Fig. 7Measurement of forces with displacement for preload of 3 KN

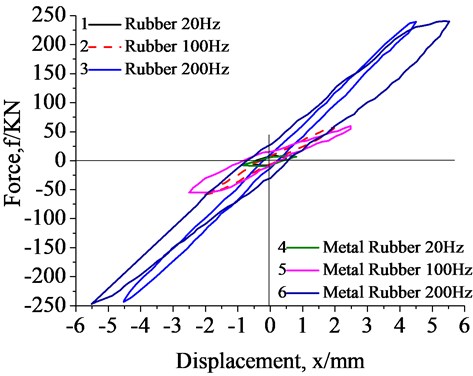
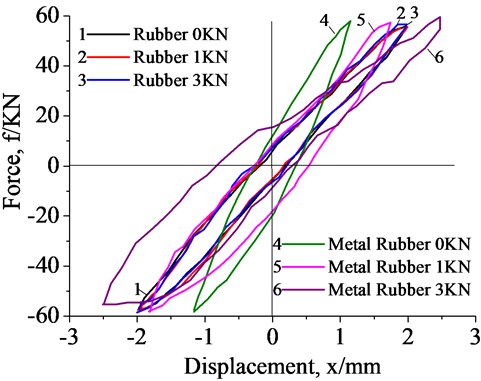
Fig. 8 displays another influence law between vibration force and displacement under different preloads at fixed frequency. The preloads of 0 KN, 1 KN and 3 KN were selected when the frequency is 100 Hz. The preloads of the both will be reduced to zero after a period of vibrating because of plastic deformations. The isolation characteristics of the three preload data represent the complete loose phase, normal operation phase and initial phase respectively. The results show that the area enclosed by the hysteretic curve of the metal rubber is proportional to the preload while independent to the rubber.

Fig. 8Measurement of forces with displacement for vibration frequency of 100 Hz

4. Stiffness characteristics analysis

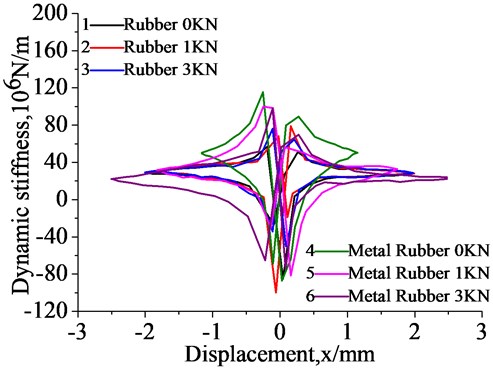
Fig. 9 and Fig. 10 represents dynamic stiffness under different vibration frequencies and preloads respectively. We can conclude that the maximum stiffness of the rubber isolator and the metal rubber isolator simultaneous reach 0 mm. The dynamic stiffness of two kinds of isolators increase as the frequency rises. The dynamic stiffness of the rubber isolators change little under different preloads, while the stiffness of the metal rubber decreases slightly as the preload increases.

Fig. 9Dynamic stiffness under different vibration frequency

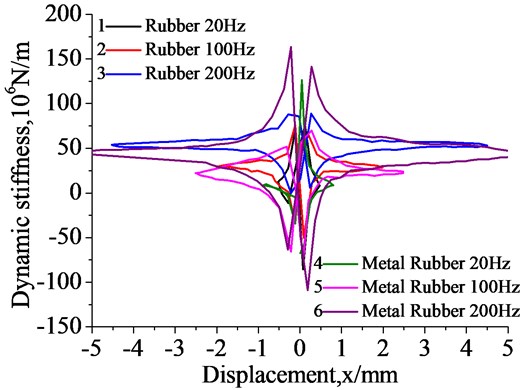
Fig. 10Dynamic stiffness under different preload

5. Conclusion

The aim of this paper is to find the difference between the rubber and the metal rubber respectively for sonic driller. The dynamic stiffness and the damping are theoretically and practically related to loading rate, preload, structural properties. The stiffness and the damping change nonlinearly with the external load. According to the micro-model, the stiffness is proportional to isolator density, elastic modulus, and uniformity. In theory, the diameter of the wire influences stiffness indirectly. However, a homogeneous isolator can be easily developed when the diameter is thinner. In order to obtain an isolator with better stiffness, it is recommended that:

(1) The annular isolators of the rubber and the metal rubber are prepared by different methods. The based structure parameters of the isolators are measured. Micro-strain model is induced on the basis of the assumption of the micro-cube. The models of the rubber and the metal rubber isolators are built and analyzed on the basis of conservation of energy. The results also show that the isolator stiffness is influenced by both its own properties and external load.

(2) The experimental schemes to study the annular isolators under quasi-static loading are designed. The stiffness characteristics test under different loading rates, loading forces and other loading states have been accomplished. The test shows that the metal rubber has great plastic deformation under loading while the rubber does not. This is resulted from a bad uniformity. The damping of the rubber and the metal rubber decrease at the same time because of the slip resulted from friction. If the loading rate is over exerted, there will be no time for the unit to deform, which leads to the damping property decrease. The total deformation of the metal rubber isolator is smaller than the rubber isolator.

(3) The dynamic stiffness of the metal rubber isolator is closely proportional to vibration frequency. Because of the uniformity, the dynamic stiffness of the rubber is maintaining stability under different preloads, while the stiffness of the metal rubber decreases with the increase of the preload. It is bigger cumulative deflection that leads to the calculation error in stiffness.

References

Sun X. B. Test methods of rubber element’s dynamic and static characteristic. Masteral Thesis, Liaoning Institute of Technology, Jinzhou, 2007, (in Chinese).

Search CrossRef
Dai D. P. Industrial application of damping technology. Tsinghua University Press, BeiJing, 1991, (in Chinese).

Search CrossRef
Zarzour M., Vance J. Experimental evaluation of a metal mesh bearing damper. Journal of Engineering for Gas Turbines and Power, Vol. 122, Issue 2, 2000, p. 326-329.

Search CrossRef
Al-Khateeb E. M. Design, modelling and experimental investigation of wire mesh vibration dampers. Ph. D. Thesis, Texas A & M University, Texas, 2002.

Search CrossRef
Ertas B. H., Luo H. G. Nonlinear dynamic characterization of oil-free wire mesh dampers. Journal of Engineering for Gas Turbines and Power, Vol. 130, Issue 3, 2008, p. 032503-1-8.

Search CrossRef
Li Y. Y., Huang X. Q. Static characteristics for metal-rubber structure with different shape factor. Chinese Journal of Applied Mechanics, Vol. 26, Issue 1, 2009, p. 82-86, (in Chinese).

Search CrossRef
Li Y. Y., Huang X. Q., Mao W. X. Investigation on the computational method of vibration response of dry friction system with cubic nonlinearity for metal rubber. Journal of Aeronautical Materials, Vol. 24, Issue 6, 2004, p. 56-61, (in Chinese).

Search CrossRef
Li Y. Y., Huang X. Q., Song K. Contacting mechanism of nonlinear friction pair for metallic rubber and its simulation results. Journal of Vibration and Shock, Vol. 30, Issue 7, 2011, p. 77-82, (in Chinese).

Search CrossRef
Li Y. Y., Huang X. Q. Nonlinear stiffness of metal-rubber. Acta Armamentarii, Vol. 29, Issue 7, 2008, p. 819-825, (in Chinese).

Search CrossRef
Gong X. S., Xie Z. J., Luo Z. H. The characteristics of a nonlinear damper for vibration isolation. Journal of Vibration Engineering, Vol. 14, Issue 3, 2001, p. 334-338, (in Chinese).

Search CrossRef
Ao H. R., Jiang H. Y., Xia Y. H. Simplified description method of elasto-hysteresisloop of metal rubber material. Journal of China University of Mining & Technology, Vol. 33, Issue 4, 2004, p. 453-458, (in Chinese).

Search CrossRef
Hou J. F., Bai H. B., Li D. W. Test research of damping performance of metal rubber damper at high-low temperature. Journal of Aeronautical Materials, Vol. 26, Issue 7, 2006, p. 50-55, (in Chinese).

Search CrossRef
Qian C. Z., Tang J.S. Bifurcation control for a non-autonomous system with two time delays. Acta Physica Sinica, Vol. 55, Issue 2, 2006, p. 617-622, (in Chinese).

Search CrossRef
Rong H. W., Wang X. D., Xu W., Meng G., Fang T. Bifurcation of safe basins in softening duffing oscillator under bounded noise excitation. Acta Physica Sinica, Vol. 54, Issue 10, 2005, p. 2557-2262, (in Chinese).

Search CrossRef
Jin Y. F., Xu W., Ma S. J., Li W. Stochastic resonance for periodically modulated noise in a linear system. Acta Physica Sinica, Vol. 54, Issue 6, 2005, p. 3480-3485, (in Chinese).

Search CrossRef
Lei Y. M., Xu W. Homoclinic chaos in averaged oscillator subjected to combined deterministic and narrow-band random excitations. Acta Physica Sinica, Vol. 56, Issue 9, 2007, p. 5103-5108, (in Chinese).

Search CrossRef
Ao H. R., Jiang H. Y., Yan H. Research of a metal rubber isolation system based on complex stiffness. Journal of Harbin Institute of Technology, Vol. 37, Issue 12, 2005, p. 1615-1620, (in Chinese).

Search CrossRef
Li Z. Y., Lu Z. R. Research on combined stiffness characteristic of metal rubber damper. Journal of Harbin Institute of Technology, Vol. 37, Issue 11, 2005, p. 1327-1332, (in Chinese).

Search CrossRef
Zhao C. S., Zhu S. J. Study on the static stiffness characteristics of rubber-mental ring. China Mechanical Engineering, Vol. 15, Issue 11, 2004, p. 962-967, (in Chinese).

Search CrossRef
Joseph R. M., Kirsten A. B., Scott C. P. Complex stiffness measurement of vibration damped structural elements. Proceedings of the International Modal Analysis Conference, Vol. 1, 2000, p. 391-397.

Search CrossRef
Mohan D. R., Scott G., Dave G. Measurement of dynamic parameters of automotive exhaust hangers. SAE Technical Papers, Noise and Vibration Conference and Exposition, Vol. 1, 2001, p. 1-8.

Search CrossRef
Bloss B., Mohan D. R. Measurement of damping in structures by the power input method. Experimental Techniques, Vol. 26, Issue 3, 2002, p. 30-32.

Search CrossRef
He S. P., Tang W. L., Fan J. Wave propagation and attenuation in a viscoelastic cylindrical tube with specific boundary. Journal of Ship Mechanics, Vol. 9, Issue 3, 2005, p. 126-136.

Search CrossRef
Mu J., Rose J. L. Guided wave propagation and mode differentiation in hollow cylinders with viscoelastic coatings. The Journal of the Acoustical Society of America, Vol. 124, Issue 2, 2008, p. 866-874.

Search CrossRef
Jia H., Jing M., Joseph L. R. Guided wave propagation in single and double layer hollow cylinders embedded in infinite media. The Journal of the Acoustical Society of America, Vol. 129, Issue 2, p. 691-700.

Search CrossRef
Ladislav P., Ludek P., Frantisek V., Jan C. Laboratory measurement of stiffness and damping of rubber element. Engineering Mechnic, Vol. 14, Issue 1, 2007, p. 13-22.

Search CrossRef
Ciambella J., Paolone A., Vidoli S. A comparison of nonlinear integral based viscoelastic models through compression tests on filled rubber. Mechanics of Materials, Vol. 42, Issue 10, 2010, p. 932-44.

Search CrossRef
Hill J. M. Radial deflections of rubber bush mountings of finite lengths. International Journal of Engineering Science, Vol. 13, Issue 4, 1975, p. 407-409.

Search CrossRef
Peng B., Zhu S. J. Eeact radial stiffness of rubber bush mountings with finite lengths. Engineering Mechanics, Vol. 26, Issue 4, 2009, p. 202-207, (in Chinese).

Search CrossRef
Horton J. M., Gover M. J., Tupholme G. E. Stiffness of rubber bush mountings subjected to radial loading. Rubber Chemical Technology, Vol. 73, Issue 1, 2000, p. 253-264.

Search CrossRef
Horton J. M., Tupholme G. E. Approximate radial stiffnessof rubber bush mountings. Material & Design, Vol. 27, Issue 3, 2006, p. 226-229.

Search CrossRef
Han D. B., Song X. G. Expermental study on constitutive model for damping and stiffness of a rubber isolato. Vibration and Shock, Vol. 28, Issue 1, 2009, p. 156-160, (in Chinese).

Search CrossRef
Huang Y. Y., He L., Tan B. Experimental research on the shock characteristics of rubber isolators. Vibration and Shock, Vol. 25, Issue 1, 2006, p. 156-160, (in Chinese).

Search CrossRef
Han D. B., Song X. G. Expermental study on constitutive model for damping and stiffness of a rubber isolator. Vibration and Shock, Vol. 28, Issue 1, 2009, p. 156-160, (in Chinese).

Search CrossRef
Yan H., Jiang H. Y., Li M. X. Static experimental research of mechanical characteristics of metal rubber under spatial loading. Journal Functional Materials, Vol. 36, Issue 6, 2005, p. 937-942, (in Chinese).

Search CrossRef
Yan H., Jiang H. Y., Liu W. J. Analysis of acceleration response of metal rubber isolator under random vibration. Acta Physica Sinica, Vol. 59, Issue 6, 2010, p. 4065-4070, (in Chinese).

Search CrossRef
Yan H., Jiang H. Y., Liu W. J. Identification of parameters for metal rubber isolator with hysteretic nonlinearity characteristics. Acta Physica Sinica, Vol. 58, Issue 8, 2009, p. 5238-5243, (in Chinese).

Search CrossRef
Wang Y., Liu B. L., Lei Y. R. Effect of loading speed on the damping performance of metal rubber material. Rare Metal Materials and Engineering, Vol. 41, Issue S2, 2012, p. 381-383, (in Chinese).

Search CrossRef
Wu G. L. The development of sonic drilling technology and its applications. Exploration Engineering, Drilling & Tunneling, Vol. 31, Issue 3, 2004, p. 39-41, (in Chinese).

Search CrossRef
Wang Y., Liu B. L., Zhou Q. Design and study for hydraulic system of sonic vibration driller. Machine Tool and Hydraulic, Vol. 40, Issue 23, 2012, p. 76-79, (in Chinese).

Search CrossRef
Xiong Y. C. The research on the mechanism of the sonic drilling technology. Masteral Thesis, China university of Geosciences, Beijing, 2007, p. 8-25, (in Chinese).

Search CrossRef
Wang Y., Liu B. L., Zhou Q. The development and research of the sonic drilling rig driven by the dual-eccentric shaft. China mechanical Engineering, Vol. 23, Issue 17, 2013, p. 2283-2288, (in Chinese).

Search CrossRef
Yu Wang, Baolin Liu, Qin Zhou Design of a sonic drill based on virtual protype technology. Transactions of the Canadian Society for Mechanical Engineering, Vol. 37, Issue 2, 2013, p. 185-196.

Search CrossRef

About this article

Received

08 September 2013

Accepted

21 December 2013

Published

31 March 2014

Keywords

rubber

metal rubber

dynamic stiffness

comparison

sonic vibration drilling

Acknowledgements

The authors gratefully acknowledge the support by the National Natural Science Foundation of China (Grant No. 51004086), the Fundamental Research Funds for the Central Universities (Grant No. 2652011273), Research Fund for the Doctoral Program of Higher Education of China (Grant No. 20100022120003) and the open Funds of Key Laboratory on Deep Geo-Drilling Technology, Ministry of Land and Resources (Grant No. NLSD201212). Meanwhile, great thanks also go to former researchers for their excellent works, which give great help for our academic study.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.