Abstract
Shadow moiré method is often used in various areas for measurement of displacements, such as orthopedics, PCB warpage measurement and others. In this article, we propose a method for quality assessment of book covers using shadow moiré technique. Qualitative and quantitative approaches are used to estimate the quality of the book cover. In order to get a qualitative estimation, a manual count of fringes indicates a presence of the distortions of the book cover. In the second case, quantitative estimation of the displacements on the book cover can be made by applying centerline identification technique.
1. Introduction
Various methods can be used for out-of-plane deformation measurement such as holographic interferometry, speckle photography, electronic speckle pattern interferometry, and moiré topography.
Two moiré topography methods are common for measuring out-of-plane displacements – shadow moiré and projection moiré [1-2]. Both methods are commonly used to measure the profile of surfaces in order to evaluate displacements caused by temperature, humidity, mechanical load, or other variables of diffusely reflecting objects. Because its optical arrangement is cheap and easy to implement in industry environment, the technique has been well studied and widely used in various field like structural mechanics, impact testing and vibration measurement [3]. In case of a standard projection moiré the projection grating is placed in front of the light source and the reference grating is placed in front of the camera. In case of the shadow moiré technique a grating is placed close to the object and its shadow is observed through the grating. The interfere s between grating lines and the shadow lines produces interference fringes. Centerlines of these interference fringes represent surface contours.
Shadow moiré technique is frequently used as a technique for evaluating component warpage. Improvements to the metrology have increased its usefulness for evaluating various board-level manufacturing technologies [4].
Application of shadow moiré technique for quality assessment of book covers is proposed in this article. Qualitative and quantitative approaches can be used to estimate the quality of the book cover. Qualitative approach is used to only determinate if warpage of a book cover has occurred. A quantitative approach allows to measure deformations of the book cover. It is accomplished by identifying centerlines of interference fringes which define the profile of the book cover.
The article is structured as follows. The basic principles about shadow moiré technique are given in Section 2. An overview of experimental setup is given in Section 3. Details about identification of moiré fringes are given in Section 4. Finally, concluding remarks are given in Section 5.
2. The shadow moiré technique
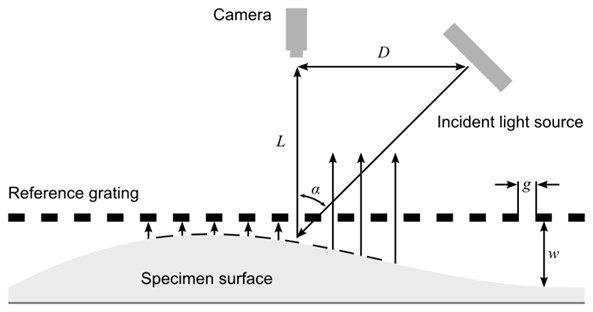
Most common shadow moiré setup based on [5] is shown in Fig. 1. A linear reference grating (comprised of black and transparent stripes) of pitch g is placed adjacent to the specimen surface. The specimen and grating are illuminated by an incident light source. A well-defined shadow of the reference grating is cast upon the specimen surface and interferes with a reference grating itself. Superposition of those two gratings forms a moiré pattern of interference fringes. The relationship between the fringe order and the gap is defined as:
where is the pitch of the grating; is the angle between the light source and the camera. In a case when distance from the camera to the specimen is equal to distance from the camera to light source , the relationship between the fringe order and the gap is defined as:
Fig. 1The optical scheme of shadow moiré technique
3. The experimental setup
A general view of the optical experimental setup comprising digital camera and shadow moiré system is shown in Fig. 2. A shadow moiré system contains of an incident light source (Fresnel lens), a grating of pitch 0.5. A grid of dark and transparent stripes is projected onto the surface of a book cover. The angle of the incident light is 45 degrees what ensures a satisfactory identification of the surface deformation and prevents excessive formation of shadows [6].
4. The identification of moiré fringes
The experimental image is shown in Fig. 3. From this experimental image one can make a conclusion that a warpage of the book cover exists. At least four fringes are clearly visible which indicates a displacement of 2 mm. In order to get centerlines of interference fringes (which can be later used to get a 3D profile of a book cover) a method discussed in [7] can be used.
The first step towards the identification of centerlines is the construction of a binary representation of the optical experimental grayscale image. Various thresholding techniques can be exploited for the construction of the binary representation of the original experimental image [6] thus a local thresholding method were used because of non-uniformity of lighting in original experimental image. The results of thresholding are shown in Fig. 3(b).
Fig. 2The optical experimental setup of the shadow moiré system

Thinning operation is performed in the second step. Two methods can be used to perform thinning of the projected grating. The first one is based on mid-point detection and the second one uses morphological mathematical operations. In our case a method, based on morphological mathematical operations was chosen. One should keep in mind that the execution of the thinning process may produce undesired parasitic components (spurs) around actual centerlines of moiré fringes which are caused during erosion by non-uniformities in objects. These spurs may be removed by performing the pruning operation which is also based on mathematical morphological operations. The results of thinning operation are shown in Fig. 3(c).
It is important to identify individual centerlines. To accomplish this, image should be divided into grid cells, an approximate line equation should be derived in each cell containing black pixels, contacting cells should be grouped into curves, and curves with fractures should be identified and joined.
When dividing image into grid cells, the selection of the size of the grid cell is an empirical procedure, but it should be related to the density of moiré fringes in the original optical image. The main requirement from the point of reliable functionality of the proposed algorithm is that there should be only one centerline passing through each grid cell. On the other hand a larger cell size increases the performance of the proposed method.
An approximation of line equations is done by sweeping cells of the thinned image and searching for cells containing black pixels. In case the current cell contains black pixels we try to identify the following parameters of the line crossing that cell. Hough transform [8] is the most reliable solution for robust identification of a line in this case. A variation of Hough transform – Randomized Hough transform [9] was used and then applied to every cell of the thinned image.
Grouping contacting cells is done by scanning cells from left to right and from top to bottom until a cell with approximated line equation is found. If there are cells with an assigned line in the immediate surroundings of , a nearest cell is joined to curve. We repeat scanning for surrounding cells until there are no cells available for joining.
Some curves may have fractures larger than one cell due to defects in the initial image or loss of information during the previously described steps.
The following steps should be performed in order to identify and join curves with fractures:
i) Select a curve from the set .
ii) Compute criteria of distance and angles between curves and ; for all available edges.
iii) Merge all cells of the curve with for such and that distance and angle criteria values are the most fit. Remove from the set and repeat steps (ii-iii) until there are no more favorable connections.
iv) Proceed with the curve and repeat steps (i-iii).
A more detailed procedure of the algorithm can be in [7]. The final results of the described procedure are shown in Fig. 3(d). It can be seen from the results that an algorithm is not able to join curves in cases when fringes are not well developed. Nevertheless an algorithm identified centerlines of the fringes and this information can be used further to get a three-dimensional profile of a book cover.
Fig. 3Identification of interference fringe centerlines: a) original optical experimental image, b) binary representation of experimental image, c) a result of thinning operation performed by mathematical morphological operations, d) a final result showing identified centerlines

a)

b)

c)
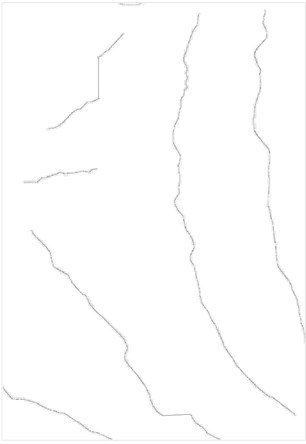
d)
5. Concluding remarks
A method for quality assessment of book covers using shadow moiré technique is presented in this paper. Qualitative and quantitative approaches are discussed. In the first case, the manual count of the interference fringes can give a qualitative estimation if the distortion of the book cover is present. In the second case, quantitative estimation of the displacements on the book cover can be made. An overview of the interference fringe identification scheme is given, which allows identification of fringe centers which can be used for identification of 3D profile. This scheme is partly based on standard algorithms of digital image processing. On the other hand, specific algorithmic implementation and original line tracing methods make this scheme robust to noise and various distortions in the original optical image. Robust identification of fringe centerlines is particularly important in shadow and projection moiré applications where it is common that poor illumination conditions, non-uniform distribution of moiré fringes in the observation area, complex surfaces of the investigated systems and noisy backgrounds do not allow a reliable interpretation of optical measurement results.
References
-
Meadows D., Johnson W., Allen J. Generation of surface contours by moiré patterns. Applied Optics, Vol. 9, Issue 4, 1970, p. 942-947.
-
Takasaki H. Moire topography. Applied Optics, Vol. 9, Issue 6, 1970, p. 1467-1472.
-
Hubing D., Jianhua W., Hong Z.,Pingping Jiab Calibration of the high sensitivity shadow moiré system using random phase-shifting technique. Optics and Lasers in Engineering, Vol. 63, 2014, p. 70-75.
-
Geng P., et al. Application of shadow moiré technique to board level manufacturing technologies. 56th Conference on Electronic Components and Technology, 2006.
-
Sharpe Jr., William N. Springer Handbook of Experimental Solid Mechanics. Springer, 2008.
-
Ragulskis M., Navickas Z. Interpretation of fringes produced by time-averaged projection moiré. Strain, Vol. 47, 2011, p. e357-e370.
-
Palevicius P., et al. A robust scheme for the identification of centerlines of moiré fringes from optical experimental images. Journal of Vibroengineering, Vol. 11, Issue 4, 2011.
-
Duda R. O., Hart P. E. Use of the Hough transformation to detect lines and curves in pictures. Communications of the ACM, Vol. 15, 1972, p. 11-15.
-
Xu L., Oja E., Kultanen P. A new curve detection method: Randomized Hough transform (RHT). Pattern Recognition Letters, Vol. 11, 1990, p. 331-338.
