Abstract
Determining age in motors and rotating machinery in general is a serious question. Using the vibration signals collected during motor aging is challenging due to nonlinear and non-stationary nature of these signals. This paper presents a study on applicability of Hurst analysis in motor vibration data collected in an artificial aging process, which at first seems to suggest inapplicability of Hurst Exponents in motor age determinations. Conclusions drawn from the straightforward application of Hurst exponent calculation are used to propose a novel method for Hurst analysis of such signals, named Higuchi-Hurst-Hilbert Vibration Decomposition (H³VD), using Higuchi’s algorithm for Hurst exponent calculation and Feldman’s Hilbert Vibration Decomposition overcoming the shortcomings of the original approach and delivering results that were expected based on previous research on frequency domain features of motor vibration in artificial aging processes. Features of this approach have been presented on both Fractional Gaussian noise model and the real vibration data. Non-accelerated bearing aging vibration data was used to demonstrate practical applicability of this new method.
1. Introduction
Motor vibration is one of characteristic signals often used for diagnostics and preventive maintenance of machinery [1], together with indicators based on sound and stator current. In case of bearing faults, well-known approach based on the defect frequencies is a classical method used for fault detection [2], but other methods have been developed in order to give answers to more complex questions such as graveness of the defect and remaining useful life (RUL) [3]. These methods have been subject to both theoretical and practical treatment in previous years.
In case of accelerated aging, motor condition at each phase of it is supposed to represent state of motor at a certain age in its life cycle [4]. Therefore, conclusions made on data from artificial aging should correspond to the real life cycle, with damage inflicted on the motor corresponding to different bearing and shaft faults and failures, unlike controlled damaging processes in which only strictly defined types of bearing faults are inflicted and their effects recorded.
In the previous studies, different features of vibration in artificial aging processes were studied in terms of their applicability in motor age and damage level detection, both in time, frequency [5] and time-frequency domain [6]. It is also important to note that in vibration analysis applied to fault detection and age determination, often a decomposition of the vibration signals is employed, the most often used being Wavelet Transform, Hilbert Huang Transform or a recent one, Hilbert Vibration Decomposition. These decompositions may act as filters of noisy components within the signal (wavelets), or to prepare the signal for application of Hilbert Transform for finding the instantaneous frequency (Hilbert Huang Transform, Hilbert Vibration Decomposition). Finally, Hilbert Vibration Decomposition aims at producing components that correspond to physical oscillators within the complex vibrating system.
This study presents a successful application of Hurst exponent’s analysis to motor age determination in accelerated aging. In order to demonstrate applicability of Hurst exponents, a new approach to it called the Higuchi-Hurst-Hilbert Vibration Decomposition (H³VD) is developed and tested on both generic and real data. It uses Hilbert Vibration Decomposition to suggest the relationship of Hurst exponent’s analysis with the basic components of the vibration, rather than the whole vibration signal.
The study is the first thorough discussion of Hurst analysis in terms of artificial motor aging vibration signals with positive applicability results, promising generality to a wider class of motor age determination problems to follow in future work. It also links results obtained in this research with other analogous results noted in frequency domain properties of vibration in artificial motor aging processes. In that manner, this paper is partially filling a knowledge gap between rescaled range analysis and classical spectral analysis as well, suggesting a tight relationship between them.
Second section of the paper presents the theory behind Hurst analysis and additional techniques employed in this paper, finally defining the H³VD. Third section presents results of H³VD application to generic and artificial motor aging vibration data. Fourth section presents an interesting application to non-accelerated aging of bearings. The fourth section draws conclusions from the study, while suggesting possible future work building on this result.
2. Methodology
(Hurst exponent, self-similarity coefficient [7]) is described by the asymptotic relation:
Here, is the rescaled range ( is difference between maximum and minimum term in the time series and is the standard deviation). For 0.51 it is said that process has long-range dependence, for 0.5 it is uncorrelated, while for 00.5 the process has short-range dependence. In simple terms, this means that high values of correspond to processes which highly depend on previous values and have memory (persistent) while low values express the opposite, being anti-trended (anti-persistent). Hurst originally used this limit as a method of Hurst exponent calculation in his work on yearly Nile high water [7].
Different methods have been introduced after Hurst’s definition in order to calculate Hurst exponent based on a time series features, including so-called Absolute moment, aggregated variance, Higuchi and Peng methods among others [8]. The Higuchi’s method will be described later on.
An accelerated aging test that had been performed according to IEEE-Std 117 (1974) test procedures gave results in form of eight vibration time series [4]. It was conducted as a combination of fluting, thermal and chemical aging. Namely, fluting aging simulates the electrical discharge from the shaft to the bearing by externally applying shaft current of 27 A at 30 V AC for 30 minutes, while the motor runs with no load. This procedure was conducted in seven runs before the motor failed in the end of seventh one. This way, eight data sets for motor vibration were collected (first one being the initial case). Sampling frequency is 12 kHz, measurement time 10 s and an anti-aliasing filter at 4 kHz has been applied.
The Hurst exponents were previously calculated for this data [9] using Chen’s MATLAB implementation of mentioned algorithms [10] with results shown in Fig. 1 and Table 1 for four different Hurst exponent calculation algorithms. Other algorithms have resulted in at least one value of Hurst exponent outside of the [0, 1] interval and were discarded for that reason, while these four have shown the same trend in Hurst exponent change with respect to motor age. This trend indicates no regularities and no direct use for motor age detection. On the other hand, Fig. 2 represents the number of zero crossings in vibration series, as reported in [11], with the characteristic monotonicity disrupted only in case of time series 5. Bearing in mind that Hurst exponent for processes with stationary increments can be estimated as:
where is the time series length and number of zero crossings [12], one would expect the same monotonicity from Fig. to be observed in Hurst exponent plot, but since no other Hurst exponent estimation algorithm produced such monotone result, it is safe to assume that Hurst exponent estimates in Fig. 1 are relevant.
Fig. 1Hurst exponent estimation for the artificial motor aging data using absolute moment, aggregated variance, Higuchi and Peng method
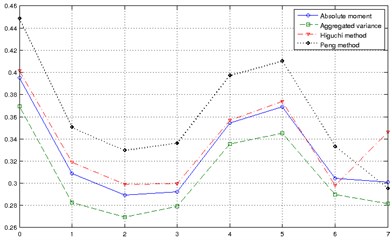
Fig. 2Number of zero crossings in respective time series
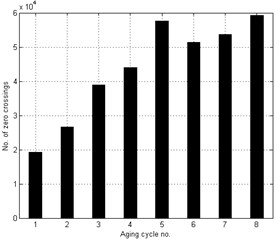
Table 1Hurst exponent estimation for the artificial motor aging data using absolute moment, aggregated variance, Higuchi and Peng method
Algorithm / cycle | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Absolute moment | 0.3951 | 0.3089 | 0.2892 | 0.2924 | 0.3546 | 0.3689 | 0.3043 | 0.3010 |
Aggregated variance | 0.3696 | 0.2825 | 0.2695 | 0.2790 | 0.3355 | 0.3451 | 0.2899 | 0.2814 |
Higuchi | 0.4016 | 0.3190 | 0.2993 | 0.2997 | 0.3569 | 0.3739 | 0.2980 | 0.3463 |
Peng | 0.4484 | 0.3505 | 0.3296 | 0.3362 | 0.3971 | 0.4101 | 0.3333 | 0.2952 |
Fact that the Hurst exponent is related to the signal spectrum and that there are various statistical features of this data set’s spectrum showing monotonicity as in Fig. 2 already discovered [11] suggests a possible monotonicity to be detected in terms of Hurst exponents. As the next section will show, the following algorithm leads to the desired result.
Step 1. Extraction of Hilbert Vibration Decomposition components, as described by Feldman [13]. The main idea is to produce signals allowing use of Hilbert Transform for instantaneous frequency calculation, but in our case this is of secondary importance. We focus on the physical interpretation of such components, since they represent the strongest harmonics in the signal.
Extraction process is based on estimating the largest energy component using synchronous detection: finding in-phase and quadrature projections of the signal and taking the square root of their sum of squares produces the desired component’s amplitude. After the first component is extracted, it is subtracted from the original signal and procedure repeats. In Feldman’s MATLAB code, it goes up to seven components, which was enough for our application as well.
Step 2. After extraction of HVD components, we apply the Hurst exponent estimation using the Higuchi’s method [8].
Higuchi method requires calculation of:
where is the time series length and block size. Since for , slope of the logarithm plot is .
Results of this simple two-step algorithm named Higuchi-Hurst-Hilbert Vibration Decomposition (H³VD) application to both motor vibration and fractional Gaussian noise data are given in the next section.
3. Results and discussion
Fig. 3 and Table 2 represent the results of applying H³VD to the vibration data. Two characteristics of this representation are obvious: the almost monotonic pattern equivalent to the one shown in Fig. 2 and linearity in Hurst exponents for the last five vibration series. Fluctuations in the first two HVD components’ order are not significant, as the sequence of components stays almost the same throughout all seven components.
This linearity deserves attention, since it could be used in this particular example as a clear indicator of motor age, emerging in all vibration series after certain level of aging. It is now an important question to raise whether this sequence and linearity occurs in a generic case.
Fig. 3H³VD applied to motor aging
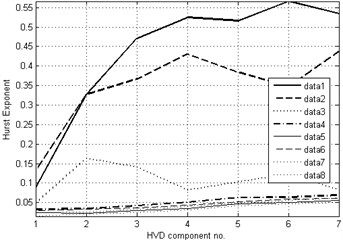
Fig. 4H³VD applied to fractional Gaussian noise
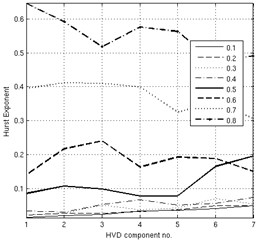
Table 2H³VD applied to motor aging
Data / Component | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
1 | 0.1870 | 0.3060 | 0.4790 | 0.4783 | 0.5408 | 0.5529 | 0.5067 |
2 | 0.1431 | 0.3512 | 0.4202 | 0.3956 | 0.3370 | 0.3778 | 0.3234 |
3 | 0.0479 | 0.1284 | 0.1606 | 0.1065 | 0.2012 | 0.1249 | 0.1479 |
4 | 0.0328 | 0.0358 | 0.0509 | 0.0479 | 0.0539 | 0.0720 | 0.0838 |
5 | 0.0180 | 0.0237 | 0.0296 | 0.0397 | 0.0445 | 0.0508 | 0.0536 |
6 | 0.0257 | 0.0309 | 0.0394 | 0.0438 | 0.0530 | 0.0568 | 0.0612 |
7 | 0.0265 | 0.0254 | 0.0329 | 0.0409 | 0.0474 | 0.0523 | 0.0580 |
8 | 0.0154 | 0.0195 | 0.0236 | 0.0317 | 0.0350 | 0.0424 | 0.0480 |
Fig. 4 presents results of the same analysis conducted on sequences of fractional Gaussian noise 100,000 samples long, with different values of from 0.1 to 0.8. It can be noted that Hurst linearity similar to the one in motor aging is observed for 0.5, characterized by small values of and linearly growing. Of course, it is important to note the general trend in which the sequence of lines follows the growing in this case, which is not observed in the real case, at least according to the Hurst exponents from Fig. 1 and Table 1.
The results of generic fractional Gaussian noise test are not tabulated for brevity, since the numerical results are not an indicator in this case.
4. Applicability of the proposed technique to rolling element bearing prognostics
The H³VD method may serve as an indicator of rolling element bearing state in normal working conditions without accelerated aging. To show this, publicly available data [14] from the setup shown in Fig. 5 was used [15]. In the experimental run which lasted eight days an AC motor was running the shaft with four bearings installed at a constant speed. The experiment terminated with the first bearing suffering outer race fault. In this study, only the data from the first accelerometer, the one installed at the first bearing was used to indicate pending fault. Accelerometers were recording a vibration signal with 1 second duration every ten minutes, at a sampling frequency of 20 kHz.
Fig. 5Experimental setup from [14, 15]
![Experimental setup from [14, 15]](https://static-01.extrica.com/articles/15187/15187-img5.jpg)
Fig. 6Linear function coefficients for H³VD components for each day
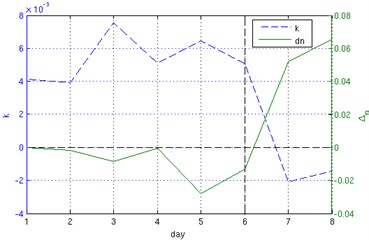
H³VD method was applied to eight vibration signals with breaks of an hour between successive ones for every day of the experiment. Mean values of Hurst exponent of corresponding HVD components in the results were taken and the resulting mean set of the Hurst exponents was linearized to a line For each day, the coefficients and are taken as representatives. Fig. 6 represents these values in function of time (days). Namely, the slope and parameter ’s increase () are shown. Reason for taking these values as indicators is simple: if we observe the diagram, it is clear that change of sign for and is implying change in the system, i.e. the bearing fault. In terms of representation of H³VD results as in Fig. 3 or Fig. 4, this means that “healthy” aging moves the linear characteristics lower and lower and keeps a positive slope, while before the breakdown, the linear characteristics start moving higher and change the slope to negative. This can be used as an indicator of pending breakdown.
5. Conclusions
The H³VD method presented in this paper demonstrates implicit applicability of Hurst analysis for age determination in an artificial aging process. It also shows Hurst linearity, a new property that may prove itself useful in applications as an indicator of faulty vibration processes.
Questions that arise at this point are both practical and theoretical in nature. Practical questions include, among others, generality of this result for all motor aging processes. This can only be addressed by further testing on other vibration data sets. Furthermore, there is a question of advantages of H³VD over other methods of statistical spectrum processing which have shown the ability to determine motor age [11]. At this point we can already state that H³VD is noise-tolerant, thanks to HVD extracting the strongest harmonics from the signal first. The characteristic Hurst linearity is an advantage as well, clearly indicating change of character in signals. Application to rolling element bearing prognostics indicates even more significance in linearity.
On the theoretical side, Hurst linearity needs an explanation, namely reasons for its occurrence. Both theoretical and practical questions formulate the direction of further research for the authors.
References
-
Nandi S., Toliyat H. A., Li X. Condition monitoring and fault diagnosis of electrical motors-a review. Energy Conversion, Vol. 20, Issue 4, 2005, p. 719-729.
-
Ocak H., Loparo K. A. Estimation of the running speed and bearing defect frequencies of an induction motor from vibration data. Mechanical Systems and Signal Processing, Vol. 18, Issue 3, 2004, p. 515-533.
-
Zhang X., Xu R., Kwan C., Liang S. Y., Xie Q., Haynes L. An integrated approach to bearing fault diagnostics and prognostics. In American Control Conference, 2005, p. 2750-2755.
-
Erbay A. S., Upadhyaya B. R., McClanahan J. P., Seker S. Accelerated aging studies of induction motors. In Proceedings of Marcon, Vol. 98, 1998.
-
Ayaz E., Şeker S., Türkcan E., Barutçu B. Combination of spectral and multi-resolution wavelet analysis for fault detection in electric motors. Third International Conference on Electrical and Electronics Engineering, Bursa, Turkey, 2003, p. 94-98.
-
Şeker S., Ayaz E. A study on condition monitoring for induction motors under the accelerated aging processes. IEEE Power Engineering Review, Vol. 22, Issue 7, 2002.
-
Hurst H. E. Long-term storage capacity of reservoirs. Transactions of the American Society of Civil Engineers, Vol. 116, 1951, p. 770-808.
-
Taqqu M. S., Teverovsky V., Willinger W. Estimators for long-range dependence: an empirical study. Fractals, Vol. 3, p. 785-798, 1995.
-
Šiljak H., Şeker S. Hurst analysis of induction motor vibrations from aging process. Balkan Journal of Electrical and Computer Engineering, Vol. 2, Issue 1, p. 16-19, 2014.
-
Chen C. Hurst parameter estimate. http://www.mathworks.com/matlabcentral/fileexchange/19148-hurst-parameter-estimate, 2008.
-
Šiljak H., Subasi A. Fourier spectrum related properties of vibration signals in accelerated motor aging applicable for age determination. Maintenance and Reliability, Vol. 16, Issue 4, 2014, p. 616-621.
-
Sinn M., Keller K. Estimation of ordinal pattern probabilities in Gaussian processes with stationary increments. Computational Statistics and Data Analysis, Vol. 55, Issue 4, 2011, p. 1781-1790.
-
Feldman M. Time-varying vibration decomposition and analysis based on the Hilbert transform. Journal of Sound and Vibration, Vol. 295, Issue 3, 2006, p. 518-530.
-
Lee J., Qiu H., Yu G., Lin J., Rexnord Technical Services. Bearing data set. IMS, University of Cincinnati, NASA Ames Prognostics Data Repository, http://ti.arc.nasa.gov/project/prognostic-data-repository, 2007.
-
Qiu H., Lee J., Lin J., Yu G. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics. Journal of Sound and Vibration, Vol. 289, Issue 4, 2006, p. 1066-1090.
About this article
The authors wish to thank Professor Belle R. Upadhyaya from University of Tennessee, Knoxville for allowing use of the motor aging data.
