Abstract
A three-dimensional finite element model is developed in order to analyze the free vibration characteristics of the tower-cable system of a triple-tower twin-span suspension bridge during the construction phase and right after the erection of the main cable. The dynamic characteristics of each component in the tower-cable system, the isolated side span, main span cables and free-standing towers, are first analyzed separately. The natural frequencies and the vibration modes of the isolated side span and the main span cables obtained from the finite element analysis closely matched the analytical solution from the linear free vibration analysis and verified the validity of the finite element model. The local natural frequency and global natural frequency were defined to categorize the characteristics of the free vibration. The calculation results show that not only does the tower-cable system maintains the information on the modal characteristics of each component in the system, but it also contains its own unique modal characteristics and other important information about the dynamics characteristics of the system. At lower natural frequency range, the swinging motion and in-plane motion are uncoupled. The coupled modal information of the towers and the cables are separated into two groups based on the natural frequencies of the vibration of the main component of the tower-cable system. Some additional natural frequencies and vibration modes are obtained from the finite element analysis depicting the dynamic interaction between the towers and the cables. Furthermore, it is observed that the lower order modes of side span cables couple with the higher order modes of the main span cables. Either in phase or out of phase, local or global modes, the tower-cable system exhibits many new coupled mode combinations that reveal useful information.
1. Introduction
In recent years, in order to meet the increasing demand for crossing long distances over water, a new era in building super long span bridges, namely multi-tower suspension bridges, has begun. In China, the first two triple tower suspension bridges, the Taizhou Yangtze River bridge and Ma’anshan Yangtze River bridge, with twin span of 1008 meter each, have just been completed and the first triple tower four span suspension bridge, the Yingwuzhou bridge, is currently under construction. Moreover, there are plans under way for building a multi-tower suspension bridge connecting Taiwan and the mainland China. The New Millennium Bridge in Korea, and the Chacao Channel Bridge in Chile, which will be finished in 2018 and 2019 on schedule respectively, are also triple tower suspension bridges.
In 1983, a comprehensive study was conducted proposing why a two adjacent suspension bridge shared with one common anchor should be adopted instead of a four-span suspension bridge, as the final alternative for the San Francisco-Oakland Bay Bridge. Niels J. Gimsing studied the stiffness characteristic of the multi-span suspension bridge, furthermore, he presented four additional types of non-traditional multi-span suspension bridges. His work was a comprehensive pioneering study on multi-suspension bridges [1]. In 1991, T. Y. Lin presented an innovative concept for bridging Gibraltar Strait, which is also a combined multi-span suspension bridge [2]. In 2001, Torben Forsberg discussed some of the specific technical aspects of multi-span suspension bridges including his own experience in the pre-design of Gibraltar Strait Crossing and Gibraltar Strait link [3]. In 2004, Osamu Yoshida investigated the deformation characteristics of a four-span suspension bridge with two main 2000 m spans and pointed out that live load deflection of the girder can be reduced to less than 1/200 of the main span length by stiffening the bending coefficient of the center tower. Based on his comprehensive research, he concluded that the four-span suspension bridge is the best, most economical solution when a deep and extra long-span water crossing is required [4].
Since only a limited number of suspension bridges with a double span longer than 1000 meter have so far been constructed and utilized, most investigations on suspension bridges reported in the literature have been limited in scope. To the best of the authors’ knowledge a comprehensive analysis considering all aspects, including the dynamic characteristics, of multi-span bridges had been lacking until Taizhou Yangtze River bridge, Ma’anshan Yangtze River bridge and New Millennium Bridge began to be designed and erected [5-10]. Moreover, no research has been reported in literature investigating the wind resistance of twin span suspension bridges during the erection period [11-15]. Investigating the dynamic performance of multi-span suspension bridges during the erection process is critically important due to the fact that many of these bridges will be built in straits frequently subjected to violent typhoon or hurricane and wind or earthquake during the construction period. Therefore, assessment of the bridge resistance to wind load during construction is more favorable than post construction state.
In this paper, the modal characteristics of tower-cable system of the twin span Ma’anshan Yangtze River bridge during the erection is studied. Vibration frequencies of the side span and the main span are compared with the results from finite element analysis to verify the accuracy of the FEM model. Subsequently, local and global frequencies are defined for convenience and to clearly describe the uncoupling of the free vibration, both in plane and out of plane. Based on these definitions the modal analysis of the single main span cable and single tower are carried out respectively in order to identify the vibration characteristics of each component in the tower cable system separately. Finally, the vibration characteristics of the tower cable system and its relationship with each single component are studied, and the unique desired modal characteristics for multi-tower cable system are clarified. This work lays down the foundation for further study on the wind resistance of multi-span bridges.
2. The finite element model
2.1. Construction details of the twin-span suspension bridge
Ma’anshan Bridge is a bridge over the Yangtze River in Ma’anshan, Anhui, China. It ties with Taizhou Bridge as the longest double span suspension bridge with a span arrangement of 360+2×1080+360 m as shown in Fig. 1.
Fig. 1General layout of Ma’anshan Yangtze River bridge (unit: m)

Two main cables of 35 m apart are made of galvanized high-tensile steel wires with a diameter of 5.2 mm and an ultimate tensile strength of 1670 MPa by prefabricated parallel-wire strands (PPWS). Each main cable consists of 154 strands and each strand weight 49T with 91 wires built into it. The outer diameter is approximately 0.688 m, and, the volume-weight and elasticity modulus of the main cable are 78.5 kN/m3 and 200 kN/mm2 respectively.
The double hanger rope is also made of high-tensile galvanized parallel wire bundles. Each hanger is composed of 109 parallel steel wires with a diameter of 5.0 mm and an ultimate tensile strength of 1670 MPa. The spacing between two adjacent hangers is 16.0 m while the separation distance from tower center to the nearest hanger is 20.0 m.
The mid-tower and two side towers are portal-type frames with two cross-beams installed between two tower legs. As Fig. 2 shows, the height of the tower is 178.8 m measured from the top surface of the pile cap to the pylon top. Besides 10.5 m decoration segment part at the top, the 127.8 m steel upper part from the bottom of the saddle downwards of the mid-tower is connected to the 40.5 m lower concrete part by the steel-concrete connection joint segments just beneath the bottom steel cross-beam. The centre-lines of the tower legs are 35 m apart at the top tower increasing to 43.5 m at the pile cap. The width of the leg is constant at 6 m in the tower plane, but in the plane of bridge tapers from 11 m at top steel-concrete joint section to 7 m at the top tower. For the pre-stressed reinforced concrete bottom tower, the widths reduces from 12 m in tower plane and 25 m in the bridge plane at the pile cap to 9.2 m and 17 m at the joint section , and, the corresponding thicknesses are 1.6 m and 2.0 m of the box section respectively, while the joint is a solid block. As for the side towers, the width of the legs are both constant at 6 m in tower plane and at 8 m in the plane of the bridge. Other dimensions are nearly the same as those of the mid-tower.
Fig. 2The principal dimension of mid-tower
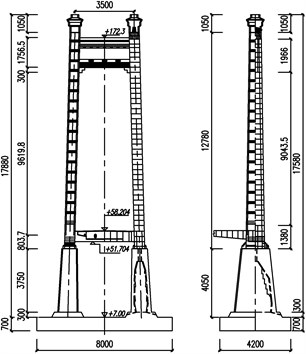
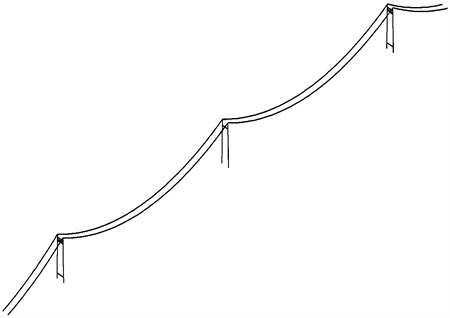
Fig. 3FEM of cable-tower system of twin span suspension bridge
2.2. Finite element modelling
A three-dimensional finite element model is established for Ma’anshan suspension bridge using MIDAS Civil (2012) software. Subsequently, the supports, girders, and the hangers are dismantled following the reverse process of the construction in order to obtain the FE model of the tower-cable system as shown in Fig. 3. In this model, three dimensional Timoshenko beam elements are used to model the thick cross-beams and legs fixed at the base of the tower. The stiffening girders are modeled with beam elements passing through the centroids of the girder sections. The anchor points of the hangers on the stiffening girders are connected to the central beam by imaginary rigid beams. All hangers and main cables are modeled with truss elements with Ernst’s equivalent elastic modulus. The model has 913 nodes and 1177 elements. The modulus of elasticity of the upper mid-tower and side towers are 210 kN/mm2 and 34.5 kN/mm2 respectively. The Poisson ratio of mid-tower is 0.3 and that of the side towers is 0.2. The volume-weight of the upper mid-tower and the side towers are 76.98 kN/m3 and 25 kN/m3 respectively [13, 16].
The tower-cable system described above is slightly modified with the consideration of the actual construction conditions associated with the completion of the erection process. For instance, the masses of the working cranes, cable saddles and platforms connected to the top of the towers are added to the corresponding nodes as additional lumped masses. The results of the static analysis of the tower-cable system show that the mid-span sag of the main span is 111.663 m which is 8.337 m smaller than that of the post construction state.
Based on this model, an extensive numerical analysis of the modal characteristics of the isolated cable, free standing tower and tower-cable coupling system are carried out and presented in the following sections.
3. Isolated cables and free-standing towers
3.1. Isolated main span cable
Due to the symmetry of the structure, only the isolated left main span cable is studied in this section. The first fifteen natural frequencies for in-plane and out-plane vibration of the isolated suspended cable based on Irvine-Caughey method [17] and FEA software respectively are tabulated in Table 1,and the mode shapes are shown in Fig. 4. As the results show, the in-plane and out-of-plane vibration modes are uncoupled. The relative difference of natural frequency between the two methods is less than 3.48 %. As can be observed from Fig. 4, the vertical component of the first in-plane vibration mode of the isolated left main span cable is antisymmetric single wave while the first mode of the out-of-plane vibration is symmetric half-wave, and the first natural frequency of in-plane vibration of the cable is almost twice the first natural frequency of out-of-plane vibration. These results are consistent with Irvine-Caughey free vibration theory [17]. The consistency between the two results above indicates the accuracy of the FE model.
Fig. 4First mode shapes of isolated main span cable

a) The first in-plane mode

b) The first out-of-plane mode
Table 1Natural frequencies of left isolated main cable
Mode no. | Natural frequency (Hz) | |||||
In-plane vibration | Out-of-plane vibration | |||||
FEM | Irvine | Difference (%) | FEM | Irvine | Difference (%) | |
1 | 0.1075 | 0.1054 | –1.95 | 0.0524 | 0.0527 | 0.52 |
2 | 0.1520 | 0.1502 | –1.17 | 0.1042 | 0.1054 | 1.17 |
3 | 0.2138 | 0.2109 | –1.38 | 0.1561 | 0.1582 | 1.33 |
4 | 0.2610 | 0.2582 | –1.08 | 0.2079 | 0.2109 | 1.43 |
5 | 0.3199 | 0.3163 | –1.11 | 0.2595 | 0.2636 | 1.54 |
6 | 0.3670 | 0.3639 | –0.86 | 0.3111 | 0.3163 | 1.64 |
7 | 0.4252 | 0.4217 | –0.82 | 0.3624 | 0.3690 | 1.79 |
8 | 0.4700 | 0.4673 | –0.58 | 0.4137 | 0.4217 | 1.91 |
9 | 0.5297 | 0.5272 | –0.48 | 0.4644 | 0.4745 | 2.11 |
10 | 0.5574 | 0.5539 | –0.64 | 0.5154 | 0.5272 | 2.24 |
11 | 0.6016 | 0.5980 | –0.60 | 0.5654 | 0.5799 | 2.50 |
12 | 0.6330 | 0.6326 | –0.06 | 0.6159 | 0.6326 | 2.64 |
13 | 0.6874 | 0.6889 | 0.22 | 0.6651 | 0.6853 | 2.96 |
14 | 0.7350 | 0.7380 | 0.42 | 0.7151 | 0.7380 | 3.11 |
15 | 0.7860 | 0.7923 | 0.80 | 0.7632 | 0.7908 | 3.48 |
3.2. Isolated side span cable
Similarly, the first ten natural frequencies for in-plane and out-plane vibration of isolated side span cable are tabulated in Table 2, and, the mode shapes are shown in Fig. 5. As can be observed from Fig. 5, the vertical component of the first in-plane vibration mode of isolated left side span cable is antisymmetric single wave, while the first mode of the out-of-plane vibration is symmetric half-wave.
The th natural frequencies of the isolated side span cable are always larger than either in-plane or out-of-plane natural frequencies of the isolated main span cable. The lower natural frequencies of the isolated side span cable are closed to the higher natural frequencies of the isolated main span cable. Therefore, it can be predicted that, in the tower-cable coupling system, some internal resonances exist between the higher vibration modes of the main span cables and the lower vibration modes of the side span cables.
For instance, because the first in-plane natural frequency, 0.3270 Hz, of the isolated side span cable is between the fifth and the sixth in-plane natural frequency of the isolated main span cable, it will excite the vibration of the side span cable during the fifth vibration mode of main span cable and turns that to the sixth vibration mode. However, the first five vibration modes of the main span cable cannot cause free vibration of the side span cable.
Fig. 5First mode shapes of isolated side span cable

a) The first in-plane mode

b) The first out-of-plane mode
Table 2Natural frequencies of left isolated side cable
Mode no. | Natural frequency (Hz) | |
In-plane vibration | Out-of-plane vibration | |
1 | 0.3270 | 0.1513 |
2 | 0.4321 | 0.3014 |
3 | 0.5856 | 0.4497 |
4 | 0.6459 | 0.5953 |
5 | 0.8098 | 0.7372 |
6 | 0.9568 | 0.9140 |
7 | 1.0945 | 1.0067 |
8 | 1.3650 | 1.2561 |
9 | 1.6584 | 1.5133 |
10 | 2.0039 | 1.7904 |
3.3. Free-standing towers
Due to the symmetry of the left and the right side tower, only the left side and the middle tower are studied herein. The first nine natural frequencies of the left side tower and the first six natural frequencies of the mid-tower, including the bending mode, torsional mode and sway mode, are listed in Table 3, and, the first bending, torsional and sway modes of the left side tower are shown respectively in Fig. 6.
From Tables 1-3, we can observe that the first sway frequency of the left side tower, 0.2589 Hz, is between the first and the second natural frequency, 0.1513 Hz and 0.3014 Hz, of the out-of-plane vibration of the side span cable, is close to the fifth natural frequency 0.2595 Hz of the out-of-plane vibration of the main span cable. The first sway frequency of mid-tower, 0.6052 Hz, is close to the twelfth natural frequency of the out-of-plane vibration of the main span cable and the fourth natural frequency, 0.5953 Hz, of the out-of-plane vibration of the side span cable. Hence, it can be predicted that the first sway mode of towers appears along with the higher out-of-plane vibration mode of the main span cables in the tower-cable system. Due to the dynamic interaction between the towers and the cables in the coupled system, the in-plane modal properties of the cables and the towers will be changed.
Fig. 6First mode shapes of free-standing left side tower

a) The first bending mode
b) The first sway mode
c) The first torsion mode
Table 3Natural frequencies of free-standing towers
Mode no. | Left side tower | Mid-tower | ||
Frequencies (Hz) | Mode type | Frequencies (Hz) | Mode type | |
1 | 0.1787 | Bending | 0.5406 | Bending |
2 | 0.2589 | Sway | 0.6052 | Sway |
3 | 0.6219 | Torsion | 1.0855 | Torsion |
4 | 1.2822 | Bending | 2.8354 | Bending |
5 | 1.4837 | Sway | 3.1002 | Sway |
6 | 1.6706 | Torsion | 3.7919 | Torsion |
7 | 3.3091 | Sway | ||
8 | 3.4790 | Bending | ||
9 | 3.9517 | Torsion | ||
4. Tower-cable system
A tower-cable system is the system when the cable erection is just finished but no girder segments are yet erected. The modal analysis shows that the swinging motion and the in-plane motion are uncoupled at a lower natural frequency range. In order to describe the modal characteristics and the dynamic interaction of the system, the in-plane vibration modes of the system are divided into the local and the global in-plane vibration modes. The local modes are further subdivided into three types that consist of the vibration of the cables only, the vibration of the cables and the side towers, and the vibration of the cables together with the mid-tower only. If all three towers vibrate together with two cables, that is defined as the global in-plane modes of vibration.
4.1. Local in-plane vibration
4.1.1. Local in-plane vibration of cables
The natural frequencies of local in-plane vibration modes for main span cables and side span cables in tower-cable system are listed in Table 4 and Table 5 respectively. Table 4 shows the first thirty-three natural frequencies of vibration modes. The fourth and eighth columns are the abbreviated description for the vibration modes of cables. For the purpose of better clarification two capital letters are defined to describe the modal combination of cables. The first letter stands for the Symmetric mode, with S, and Antisymmetric mode, with A, for any single span. The second explains the relationship between any two spans with A and C to denote Axial-symmetry and Central-symmetry modes about the mid-tower respectively.
Table 4Natural frequencies of local in-plane modes of vibration of main span cables
Mode no. | Natural frequency (Hz) | Modal property | Modal combination | Mode no. | Natural frequency (Hz) | Modal property | Modal combination |
1 | 0.1075 | in phase | AA | 18 | 0.4252 | out of phase | AC |
2 | 0.1075 | out of phase | AA | 19 | 0.5297 | in phase | AA |
3 | 0.1075 | in phase | AC | 20 | 0.5297 | out of phase | AA |
4 | 0.1075 | out of phase | AC | 21 | 0.5297 | in phase | AC |
5 | 0.1517 | out of phase | SA | 22 | 0.5620 | in phase | SA |
6 | 0.2138 | in phase | AA | 23 | 0.5625 | out of phase | SA |
7 | 0.2138 | out of phase | AA | 24 | 0.5962 | in phase | SA |
8 | 0.2138 | in phase | AC | 25 | 0.5966 | out of phase | SA |
9 | 0.2138 | out of phase | AC | 26 | 0.6330 | in phase | AA |
10 | 0.3198 | out of phase | AA | 27 | 0.6330 | out of phase | AA |
11 | 0.3198 | in phase | AA | 28 | 0.6856 | in phase | SA |
12 | 0.3199 | out of phase | AC | 29 | 0.6861 | out of phase | SA |
13 | 0.3199 | in phase | AC | 30 | 0.7340 | in phase | AA |
14 | 0.3682 | in phase | SA | 31 | 0.7354 | out of phase | AA |
15 | 0.4252 | in phase | AA | 32 | 0.7386 | in phase | AA |
16 | 0.4252 | out of phase | AA | 33 | 0.7854 | in phase | SA |
17 | 0.4252 | in phase | AC |
Comparing the data of Table 4 with the natural frequencies of isolated main span cables in Table 1, it is evident that Table 4 almost includes all the natural frequencies in Table 1. It indicates that the local in-plane vibration modes of tower-cable system still holds the modal characteristics of each component of tower-cable coupled system, but it also has new unique modal characteristics different from the isolated single cable. For example, all the first four natural frequencies in Table 4 are 0.1075 Hz, and the corresponding mode shapes of single main span cables are still single wave as the Fig. 7 shows. There are four types of modal combination, two of the modes are single span Antisymmetry with double span Axial-symmetry (AA) in-phase mode and out-of-phase mode of vibrations, the other two are single span Antisymmetry with double span Central-symmetry (AC) of in-phase and out-of-phase modes. Thus, the frequencies of tower-cable system in Table 4 can be divided into some groups according to frequencies of isolated cables in Table 1. Such as the first four natural frequencies in Table 4 according to the first in-plane natural frequency 0.1075 Hz in Table 1, the fifth natural frequency in Table 4 according to the second natural frequency 0.1520 Hz in Table 1 and the sixth to ninth natural frequency in Table 4 according to the third natural frequency 0.2138 Hz in Table 1 and so on. Similarly, from Table 5 and Table 1, the natural frequencies of local in-plane vibration of side span cables are divided into groups.
There are several coupling resonances between higher order modes of main span and the modes of side span according to Table 4 and Table 5. For instance, the first local in-plane vibration in which the corresponding natural frequency is 0.3198 Hz of side span cables excites the tenth local in-plane vibration of main span cables. However, as Fig. 8 shows, the fifteenth vibration mode of main span cable is single span Symmetric mode in which the additional tension of cable is zero which means it doesn’t excite the vibration of side span cable, thus, there is no natural frequency in Table 5 that matches that. Similarly, the natural frequency for the third vibration mode of side span cables in Table 1 does not have a corresponding frequency in Table 4.
Table 5Natural frequencies of local in-plane modes of vibration of side span cables
Mode no. | Natural frequency (Hz) | Modal property | Modal combination | Mode no. | Natural frequency (Hz) | Modal property | Modal combination |
1 | 0.3198 | out of phase | SA | 10 | 0.5966 | out of phase | SA |
2 | 0.3270 | out of phase | AC | 11 | 0.6458 | in phase | AC |
3 | 0.3271 | in phase | AA | 12 | 0.6458 | in phase | AA |
4 | 0.3271 | in phase | AC | 13 | 0.6856 | in phase | SA |
5 | 0.3276 | out of phase | AA | 14 | 0.6861 | out of phase | SA |
6 | 0.3682 | in phase | SA | 15 | 0.7340 | in phase | SA |
7 | 0.5620 | in phase | SA | 16 | 0.7354 | out of phase | SA |
8 | 0.5625 | out of phase | SA | 17 | 0.7386 | in phase | SA |
9 | 0.5962 | in phase | SA | 18 | 0.7854 | in phase | SA |
It is interesting that, along with the local in-plane vibration, all modal combinations of side span cables are single span Symmetry with double spans Axial-symmetry (SA) in Table 5. It can also be observed from Fig. 7 and Fig. 8 that the towers generate some relatively small motion when the local natural frequencies of cables are close to the local frequencies of towers or the global frequencies of the system.
Fig. 7The first four local in-plane mode shapes of main span cables

a) In phase (AA)

b) Out of phase (AA)

c) In phase (AC)

d) Out of phase (AC)
Fig. 8The local in-plane mode shapes of main span cables and side span cables
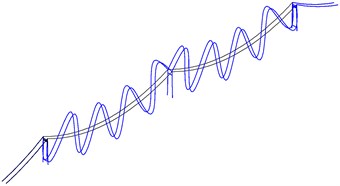
a) The fifteenth modal motion of main span cables

b) The third modal motion of side span cables
4.1.2. Local in-plane vibration of two side towers
The natural frequencies of local in-plane vibration of two side towers of tower-cable system are listed in Table 6. Affected by the main cables in the local in-plane vibration of tower-cable system, some new natural frequencies of bending mode and torsional mode of side tower are generated as compared with Table 3, and, the lower order frequencies are closely spaced. The result also shows that all the modal properties of bending mode and torsional mode of two side towers are out-of-phase in the local in-plane vibration mode of side towers, and, when bending is the dominant mode of two side towers, all the modal properties of two cables are in-phase, while when torsion is the dominant mode of two side towers all the modal properties of two cables are out-of-phase.
Table 6Natural frequencies of local in-plane modes of vibration of two side towers
Mode no. | Bending mode (out of phase) | Torsion mode (out of phase) | ||||
Natural frequency (Hz) | Two cables | Natural frequency (Hz) | Two cables | |||
Modal property | Modal combination | Modal property | Modal combination | |||
1 | 0.1465 | in phase | SA | 0.2595 | out of phase | SA |
2 | 0.1767 | in phase | SA | 0.3207 | out of phase | SA |
3 | 0.2631 | in phase | SA | 0.3693 | out of phase | SA |
4 | 0.4626 | in phase | SA | 0.4654 | out of phase | SA |
5 | 0.4814 | in phase | SA | 0.4900 | out of phase | SA |
It is interesting that, for either the bending mode or the torsional mode, all the modal combinations of two cables are single span Symmetry with double span Axial-symmetry (SA). The second bending and torsional mode of side towers in local in-plane vibration are shown in Fig. 9. It can be seen that the second bending frequency 0.1767 Hz of side towers excites the second vibration mode of main span cables and the half-wave mode of side span cable. The second torsional frequency 0.3207 Hz of side towers excites the fifth vibration mode of main span cables and the first mode of side span cable. Therefore, it can be concluded that, in the local in-plane vibration of triple-tower twin-span tower-cable system, the larger out of phase bending vibration mode of two side towers will excite the main cable as an in-phase modal combination which is single span Symmetry with double span Axial-symmetry (SA). While the larger out of phase torsional vibration of the side towers will excite a similar modal combination but out-of-phase.
Fig. 9The second local in-plane mode shapes of two side towers
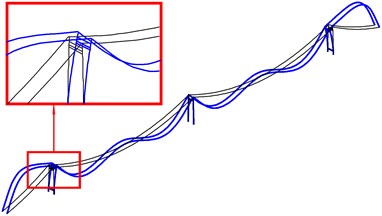
a) The second bending mode (in phase) (SA)
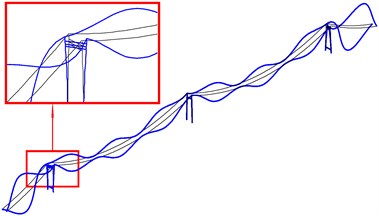
b) The second torsional mode (out of phase) (SA)
4.1.3. Local in-plane vibration of mid-tower
Table 7 lists the natural frequencies of local in-plane vibration modes for the mid-tower. Similarly, compared with table 3, some new natural frequencies of bending mode and torsional mode of side tower are generated and are closely spaced. In the local in-plane vibration modes of mid-tower, for the bending mode of mid-tower all the modal properties of two cables are in-phase, while for the torsional mode of mid-tower the modal properties of two cables are out-of-phase.
It is obvious that either for the bending modes or the torsional modes, all the modal combinations of two cables are single span Symmetry with double span Central-symmetry (SC) and the side span cables have no motion or only slight motion. Fig. 10 shows the first bending and torsional mode of the local in-plane vibration mode of mid-tower. The first bending frequency 0.3735 Hz excites the sixth vibration mode of main span cables, and, the first torsional frequency 0.1499 Hz excites the second vibration mode of main span cables while the side span cables experience almost no motion at all. Hence, it can be concluded that, in the local in-plane vibration of three-tower and two-span tower-cable system, the larger bending vibration mode of mid-tower will excite an in-phase modal combination which is single span Symmetry with double span Central-symmetry (SC) of main cables. While the larger torsional vibration will excite a similar modal combination but out-of-phase mode of the main cable.
Table 7Natural frequencies of local in-plane modes of vibration of mid-tower
Mode no. | Bending mode | Torsion mode | ||||
Natural frequency (Hz) | Two cables | Natural frequency (Hz) | Two cables | |||
Modal property | Modal combination | Modal property | Modal combination | |||
1 | 0.3735 | in phase | SC | 0.1499 | out of phase | SC |
2 | 0.4777 | in phase | SC | 0.5820 | out of phase | SC |
3 | 0.5813 | in phase | SC | 0.6838 | out of phase | SC |
Fig. 10The first local in-plane mode shapes of mid-tower
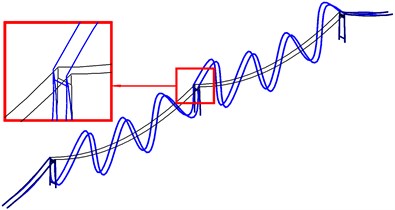
a) The first bending mode (in phase) (SC)
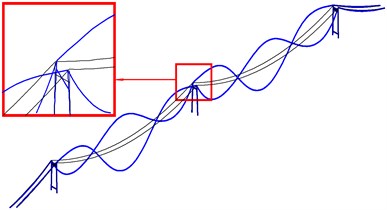
b) The first torsional mode (out of phase) (SC)
4.2. Global in-plane vibration
The natural frequencies of global in-plane vibrations are listed in Table 8. It is still clear that the lower order natural frequencies present are closely spaced. Both the bending and torsional modes of two side towers are in phase. For the bending mode the modes of cable are in phase while for torsional mode of the side tower the modes of cable are out of phase. All the modal combinations of the twin cables are single span Symmetry with double span Central-symmetry (SC). In contrast to the local in-plane vibration mode of mid-tower, the vibration of side span cables are excited in the global in-plane vibration of system due to the vibration of side towers.
The first bending and torsional mode of global in-plane vibration are shown in Fig. 11. The first bending frequency of the tower-cable system 0.1297 Hz is a new outcome just between the first and the second natural frequency of isolated main span cable, and, smaller than the first natural frequency of isolated side span cable. The fourth vibration mode of main span cables and the half-wave mode of side span cables are excited by the first torsional frequency, 0.2497 Hz, close to the fourth natural frequency of isolated main span cable. Fig. 12 shows the second bending and torsional mode of global in-plane vibration respectively. Similarly, the second vibration mode shape of main span cables and the half-wave mode shape of side span cables are excited by the second bending frequency of 0.1696 Hz. While the second torsional vibration mode excites the fifth vibration mode of the main span cables and the similar mode of the side span cables. The new frequency of the tower-cable system is the result of coupling effect of the components with each other. From Table 8, it can be observed that in global in-plane vibration of twin-span tower-cable system, large bending or torsional mode with two side towers in phase, will excite the vibrations in phase mode of two cables with the single span Symmetry and with double spans Central-symmetry (SC). As the torsional mode of the side tower is concerned, the same SC modes are excited but out of phase only. That is much more relevant to the local in-plane vibration of towers.
Table 8Natural frequencies of global in-plane modes of vibration of cable-tower system
Mode no. | Bending mode (in phase) | Torsion mode (in phase) | ||||
Natural frequency (Hz) | Two cables | Natural frequency (Hz) | Two cables | |||
Modal property | Modal combination | Modal property | Modal combination | |||
1 | 0.1297 | in phase | SC | 0.2497 | out of phase | SC |
2 | 0.1696 | in phase | SC | 0.2940 | out of phase | SC |
3 | 0.2294 | in phase | SC | 0.3625 | out of phase | SC |
4 | 0.2714 | in phase | SC | 0.3863 | out of phase | SC |
5 | 0.4901 | in phase | SC | 0.4791 | out of phase | SC |
6 | 0.5111 | out of phase | SC | |||
Fig. 11The first bending mode and torsion mode of global in-plane vibration of cable-tower system
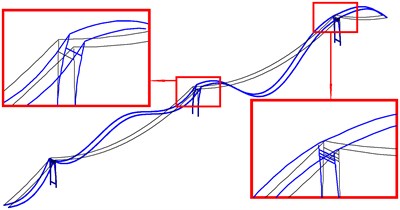
a) In phase (SC)
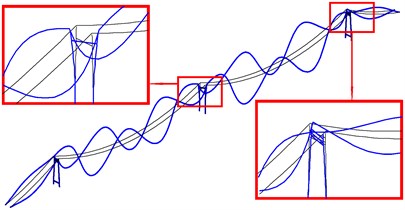
b) Out of phase (SC)
Fig. 12The second bending mode and torsion mode of global in-plane vibration of cable-tower system
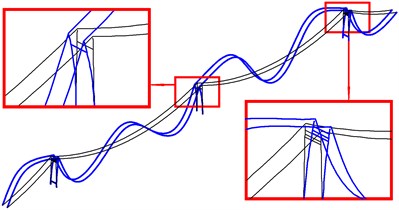
a) In phase (SC)
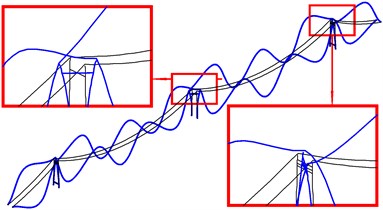
b) Out of phase (SC)
4.3. Local out-of-plane vibration
Similar to the in-plane vibration, the out-of-plane vibration of three-tower and two-span tower-cable system is divided into the local and global out-of-plane vibration. The local out-of-plane vibration is subdivided into the local out-of-plane vibration of cables, side towers and the mid-tower.
4.3.1. Local out-of-plane vibration of cables
The local out-of-plane vibration frequencies of the system are listed in Table 9 and Table 10. The natural frequencies of the local out-of-plane vibration of cables can be separated into groups according to the frequency of the isolated cables. For example, the first four natural frequencies of local out-of-plane vibrations of cables of tower-cable system can be classified into one group corresponding to the first natural frequency of out-of-plane vibration of isolated main span cables in Table 1. The first four vibration modes are the combinations of the modes of the two main span cables. It also indicates that, because the interaction of out-of-plane vibrations between cables and towers is not as strong as in the in-plane vibrations, thus, the out-of-plane vibrations of main cables still completely maintain the characteristics of isolated cables and it is combined with the unique characteristics of twin-span tower-cable system.
Table 9Natural frequencies of local out-of-plane modes of vibration of main span cables
Mode no. | Natural frequency (Hz) | Modal property | Modal combination | Mode no. | Natural frequency (Hz) | Modal property | Modal combination |
1 | 0.0522 | in phase | SA | 17 | 0.3043 | in phase | AA |
2 | 0.0524 | in phase | SC | 18 | 0.3044 | in phase | AC |
3 | 0.0524 | out of phase | SA | 19 | 0.3111 | out of phase | AA |
4 | 0.0524 | out of phase | SC | 20 | 0.3111 | out of phase | AC |
5 | 0.1038 | in phase | AA | 21 | 0.3618 | in phase | SA |
6 | 0.1040 | in phase | AC | 22 | 0.3624 | out of phase | SA |
7 | 0.1042 | out of phase | AA | 23 | 0.3624 | out of phase | SC |
8 | 0.1042 | out of phase | AC | 24 | 0.3629 | in phase | SC |
9 | 0.1554 | in phase | SA | 25 | 0.4136 | out of phase | AA |
10 | 0.1558 | in phase | SC | 26 | 0.4137 | out of phase | AC |
11 | 0.1560 | out of phase | SA | 27 | 0.4140 | in phase | AC |
12 | 0.1560 | out of phase | SC | 28 | 0.4644 | out of phase | SA |
13 | 0.2078 | out of phase | AA | 29 | 0.4647 | in phase | SC |
14 | 0.2079 | out of phase | AC | 30 | 0.5153 | out of phase | AA |
15 | 0.2595 | out of phase | SA | 31 | 0.7298 | in phase | AA |
16 | 0.2595 | out of phase | SC | 32 | 0.7632 | in phase | SA |
Nevertheless, due to the interactions of system some new natural frequencies of local out-of-plane vibrations are generated such as the first six natural frequencies of out-of-plane of side span cables in Table 10. It must noted that, due to the growing interactions with the increasing frequencies, the separation of frequencies in groups will be not apparent, as can be seen, for instance, from the 31st, 32nd frequency etc. in Table 9.
Table 10Natural frequencies of local out-of-plane modes of vibration of side span cables
Mode no. | Natural frequency (Hz) | Modal property | Modal combination | Mode no. | Natural frequency (Hz) | Modal property | Modal combination |
1 | 0.1501 | in phase | SA | 8 | 0.3044 | in phase | AC |
2 | 0.1501 | in phase | SC | 9 | 0.4497 | out of phase | SA |
3 | 0.1512 | out of phase | SA | 10 | 0.4506 | in phase | SC |
4 | 0.1512 | out of phase | SC | 11 | 0.4506 | in phase | SC |
5 | 0.1554 | in phase | SA | 12 | 0.7298 | in phase | AA |
6 | 0.1558 | in phase | SC | 13 | 0.7374 | in phase | SA |
7 | 0.3043 | in phase | AA |
4.3.2. Local out-of-plane vibration of two side towers
The natural frequencies of local out-of-plane vibration of side towers in Table 11 also appear in pairs. The sway modes of two side towers in one pair are in phase and out of phase respectively, while the modes of two cables are both in phase. For the Axial-symmetry mode of the two main cables, the mode of the side tower is in phase, while for the Central-symmetry mode of the main cables, the mode of side tower is out of phase.
From Table 3 and Table 11, we know the third and fourth natural frequencies are almost equal to the first sway frequency of the isolated cable in Table 3, while the first two and the 5th frequencies are the newly generated frequencies. This indicates that the two side towers have the modal properties of free-standing towers and generate adjacent natural frequencies due to the influence of vibration of two cables in the local out-of-plane vibration.
Table 11Natural frequencies of local out-of-plane modes of vibration of two side towers
Mode no. | Natural frequency (Hz) | Two cables | Sway mode property of side towers | |
Mode property | Mode combination | |||
1 | 0.2065 | in phase | AA | in phase |
2 | 0.2070 | in phase | AC | out of phase |
3 | 0.2512 | in phase | SA | in phase |
4 | 0.2515 | in phase | SC | out of phase |
5 | 0.3125 | in phase | AC | out of phase |
4.3.3. Local out-of-plane vibration of mid-tower
The natural frequencies of local out-of-plane of mid-tower present are not so closely spaced as the side tower are, as shown in Table 12. Affected by the vibration of cables in tower-cable system, the mid-tower has new natural frequencies near the first sway natural frequency 0.6052 Hz of free-standing mid-tower in Table 3. The mode of main cables in the local out-of-plane vibrations are all in phase and Axial-symmetry about the mid-tower. This indicates that, for the mid-tower with larger stiffness, a resonance is excited in the sway Axial-symmetry mode of the main span cables and the mid-tower near the first sway frequency of free-standing mid-tower in Table 3.
Table 12Natural frequencies of local sway modes of vibration of mid-tower
Mode no. | Natural frequency (Hz) | Two cables | |
Modal property | Modal combination | ||
1 | 0.5122 | in phase | AA |
2 | 0.5591 | in phase | SA |
3 | 0.5957 | in phase | SA |
4 | 0.5974 | in phase | SA |
5 | 0.6171 | in phase | AA |
6 | 0.6275 | in phase | AA |
7 | 0.6695 | in phase | SA |
8 | 0.7171 | in phase | AA |
9 | 0.7864 | in phase | AA |
10 | 0.8160 | in phase | SA |
4.4. Global out-of-plane vibration
Table 13 lists the natural frequencies of global out-of-plane vibration of the tower-cable system. It is interesting that the sway natural frequencies of the system are just between the first sway natural frequency of the side tower and the mid-tower. The modes of two cables are in phase Axial-symmetry modes. Thus, the sway modal properties of two side towers must be in phase and the corresponding natural frequencies always excite the out-of-plane vibration of the mid-tower. Subsequently, with the interactions between three towers and two cables, the sway natural frequencies of two side towers and the mid-tower tend to couple. This results in increasing the sway natural frequencies of the side towers and decreases the sway natural frequencies of the mid-tower.
From the above modal analysis, we conclude that the in-plane and out-of-plane dynamic response of the tower-cable system to wind excitation should be computed using the coupled system model rather than the separate free-standing tower model and isolated model. As the interaction relationship between the towers and the main cables indicate, the natural frequencies of the tower-cable system are more closely spaced and are lower than those of the free-standing towers. The cross-correlation terms and the higher modes may have to be taken into account as the wind response is considered.
Table 13Natural frequencies of global out-of-plane modes of vibration of cable-tower system
Mode no. | Natural frequency (Hz) | Two cables | Sway modal property of side towers | |
Modal property | Modal combination | |||
1 | 0.3116 | in phase | AA | in phase |
2 | 0.4125 | in phase | AA | in phase |
3 | 0.4626 | in phase | SA | in phase |
The modes of the cable-tower system are categorized and described in details, and important issues such as modal combination problems have been elaborated. However, for the initial curvature and stretching parameters of the cables being neglected, the nonlinearity effects due to quadratic and cubic items were not introduced into the cable-tower dynamic system above. It is speculated and possibly expected that more nonlinear characteristics such as internal resonance or mode bifurcation may develop when certain conditions such as yielding the inner resonance is satisfied, for the twin-span suspension bridge with large span is always a flexible structure especially in the construction period. The complex nonlinear modal effects will be subject of further research by the authors.
5. Conclusions
By considering and taking into account the conditions and the parameters encountered in the construction process, a three-dimensional dynamic finite element model is established to analyze the modal characteristics of the free vibration of the tower-cable system of a triple tower twin span suspension bridge during the construction process and after the main cable erection is completed. The results indicate that not only the tower-cable system still maintains the modal characteristics of the components of the tower-cable coupling system, but it also has its own unique modal characteristics. The swinging motion and the in-plane motion of the coupled system are uncoupled in lower natural frequency range.
Based on the frequency of the isolated tower or the cables, the combination mode of the tower-cable system can be categorized into several distinct groups. The system generates several new natural frequencies and vibration modes because of the dynamic interaction between the towers and the cables, and, the lower order modes of side span cables couple with the higher order modes of the main span cables, either in phase or out of phase, local or global modes. The tower-cable system exhibits many new mode combinations.
The modal analysis of the tower-cable system of triple-tower twin-span suspension bridge reveals some new characteristics for free vibration of multi-span tower-cable coupled systems, and it is useful for further study on the wind excited dynamic response of multi-span bridges during the erection period.
References
-
Niels J. Gimsing Cable Supported Bridges: Concept and Design. John Wiley & Sons, 1st edition, 1983.
-
Lin T. Y., Chow Philip Gibraltar strait crossing-a challenge to bridge and structural engineers. Structural Engineering International, Vol. 1, Issue 6, 1991, p. 53-58.
-
Forsberg T. Multi-span suspension bridges. International Journal of Steel Structures, Vol. 1, Issue 1, 2001, p. 63-73.
-
Yoshida O., Okuda M., Moriya T. Structural characteristics and applicability of four-span suspension bridge. Journal of Bridge Engineering, Vol. 9, Issue 5, 2004, p. 453-463.
-
Jennings A. Gravity stiffness of classical suspension bridges. Journal of Structural Engineering, Vol. 109, Issue 1, 1983, p. 16-36.
-
Xiheng Luo, Dazhang Han, Tianbao Wan Deflection theory and its programming for multi-tower suspension bridges. Bridge Construction, Vol. 41, Issue 2, 2008, p. 41-44, (in Chinese).
-
Yang Jin Technical feasibility and advantages of applying multi-tower and multi-span suspension bridge to construction of long bridge across straits. Bridge Construction, Vol. 36, Issue 2, 2009, p. 36-39, (in Chinese).
-
Deng Ting, Luo Xiheng Study for reasonable value of friction coefficient between main cable and saddle. Engineering Sciences, Vol. 10, Issue 3, 2012, p. 72-76, (in Chinese).
-
Dong-Ho Choi, Sun-Gil Gwon, Hoon Yoo, Ho-Sung Na Nonlinear static analysis of continuous multi-span suspension bridges. International Journal of Steel Structures, Vol. 13, Issue 1, 2013, p. 103-115.
-
Huu-Tai Thai, Dong-Ho Choi Advanced analysis of multi-span suspension bridges. Journal of Constructional Steel Research, Vol. 90, 2013, p. 29-41.
-
Xinjun Zhang Investigation on aerodynamic stability of long-span suspension bridges under erection. Journal of Wind Engineering and Industrial Aerodynamics, Vol. 92, Issue 1, 2004, p. 1-8.
-
Ge Y. J., Xu L. S., Zhang W. M., Zhou Z. Y. Dynamic and aerodynamic characteristics of new suspension bridges with double main spans. In Seventh Asia-Pacific Conference on Wind Engineering, Taipei, Taiwan, 2009, p. 177-180.
-
Wenming Zhang, Yaojun Ge, Marc L. Levitan Nonlinear aerostatic stability analysis of new suspension bridges with multiple main spans. Journal of the Brazilian Society of Mechanical Sciences, Vol. 35, Issue 2, 2013, p. 143-151.
-
Xu Y. L., Ko J. M., Yu Z. Modal analysis of tower-cable system of Tsing Ma long suspension bridge. Engineering Structures, Vol. 19, Issue 10, 1997, p. 857-867.
-
Xu Y. L., Ko J. M, Zhang W. S. Vibration studies of Tsing Ma suspension bridge. Journal of Bridge Engineering, Vol. 2, Issue 4, 1997, p. 149-156.
-
Anhui Provincial Highway Design Institute (APHDI) and China Major Bridge Reconnaissance and De-sign Institute (CMBRDI) (2008). Documents of Preliminary Design of Anhui Maanshan Bridge, (in Chinese).
-
Irvine H. M. Cable Structures. Dover Publications, In New York, The Massachusetts Institute of Technology Press, 1981, p. 91-93.
About this article
The work reported is supported by a project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.
