Abstract
This paper describes the application of the local Hölder exponent which can measure sensitive features associated with nonstationary and nonlinearity. By investigating in detail the structure and the main properties of the local Hölder function, a fault diagnosis technology is developed on the basis of error function. The study is conducted for both engines of two Boeing 737 commercial aircrafts as a measure the regularity of aeroengine time series. In order to accurately detect the impending aeroengine faults, the Hölder exponent estimation is performed for comparative analysis of the aeroengine records. Using this analysis, the difference between left and right engine is obvious when one of the engines is fracture failure.
1. Introduction
In recent years, the fractal and multifractal theory has been studied widely to measure the regularity of time series. The local Hölder exponent, as an important tool in multifractal analysis, provides information about the regularity of a signal [1-4]. But other characterizations of local regularity exist, such as the pointwise Hölder exponent, the oscillation exponents, the fluctuation exponents, Hausdorff dimensions and the degree of fractional differentiability [5, 6]. We shall mainly be concerned in this paper with the study of the local Hölder exponent.
The pointwise Hölder exponent can pertain to the global regularity of a signal, which can be found through the use of the Fourier transform [7]. Unfortunately, the Fourier transform approach cannot be used to find the regularity at a particular point in time. On the other hand, Wavelets are well localized in time and can therefore provide an estimate of the Holder regularity both over time intervals and at specific time points. The formalism, by applying the wavelet transform representation of a signal to multifractal analysis, developed by Arneodo et al in the early nineties [8, 9] has been extensively used to test many natural phenomena and has contributed to substantial progress in each domain in which it has been applied [10-12].
The Hölder exponent has proven to be a useful tool for time series analysis [10, 13] and also have been used in some applications of health monitoring. By fitting an autoregressive moving average (ARMA) model to the wavelet-transformed data, analysis of the Hölder exponent based on wavelet transform is used to indicate the presence of fatigue cracks in gears [3]. By using the wavelet modulus maxima method, the Hölder exponent is used to examine shaft orbits [4].
In this paper, we would notice the Hölder regularity, quantifies the amount of regularity any given point on a signal, using known Hölder exponent [10, 13-15]. Nevertheless the pointwise Hölder exponent provides only global estimates of scaling, while there are cases when local information about scaling provides more relevant information than the global spectrum. Therefore, we address the problem of estimation of the local scaling exponent. Here we first investigate the fractal scaling characteristic of aeroengine dynamics from normal engine by applying the local Hölder exponent method. And then, we obtain the fractal scaling properties of signals from the fracture failure in engine, and compare the difference in the fractal scaling results. To this end, we define error function between the Hölder exponent of original data for left and right engine. The results indicate that the fracture failure engine data can be discovered.
The structure of the paper is as follows. In section 2, we focus on the flight data and the Hölder exponent analysis. In section 3, we introduce a technique named fractal comparative diagnostics analysis method enabling us to estimate the parameter characteristic for aeroengine. In particular, the ability to distinguish between normal and abnormal signals in engine is demonstrated by two aircraft. The conclusion of the paper is drawn in section 4. Based on the fractal theory and comparative analysis, this paper presents applications of the proposed technique to the aeroengine data.
2. Methodology and algorithm
2.1. EGT data acquisition and signal processing
Data available from commercial 737 aircrafts are used for this paper. The 737 aircraft data includes operational flight data from on-board flight data recorders. These recorders are part of the Aircraft Condition Monitoring System (ACMS) such as Smart ACMS Recorder (SAR) and Quick Access Recorder (QAR).
SAR data records specific flight parameters on preset data recording channels. But the QAR data is a more comprehensive that data includes an extensive list of flight parameters recorded at specific sampling intervals which are set by the manufacturer. Moreover, the set of data includes engine reports which are generated when selected parameters meet certain predefined conditions during a particular flight phase. Furthermore, the data also includes baseline values for a subset of flight parameters and the respective threshold operating values for these parameters. In addition the series information can come in handy to decide at what stage during a flight, the parameters corresponding to a system or sub-system reach abnormal operating conditions. Therefore, the QAR data is applied in this paper.
By applying flight condition data and situational parameters, diagnostic and prognostic schemes can be developed which contribute to determining engine behavior during a specific flight and predict engine performance by estimating the flight parameter conditions of future flights. Various flight parameters such as Exhaust Gas Temperature (EGT), Fuel Flow (FF), Engine Fan Speeds (N1 and N2) are usually used to estimate the engine health and performance [16].
2.2. Analytical method
The aeroengine dynamics have to be considered as nonstationary. Therefore, most of the widely used signal processing techniques based on the assumption of stationarity and globally characterise signals are not fully suitable for detecting short-duration dynamic phenomena [17]. Thus, we address the problem of estimation of the local scaling exponent.
For convenience, we describe briefly the Hölder exponent firstly. Given a function with a singularity at time , the Hölder exponent defined as the supremum exponent such that there exists polynomial of order satisfying [8-11]:
where in the neighborhood of , and is a constant. is often associated with the Taylor expansion of around , but Eq. (1) is valid even if such expansion does not exist [18]. The Hölder exponent is therefore a function defined for each point of , and it describes the local regularity of the function . By selecting properly a wavelet kernel that is orthogonal to polynomials up to degree , the continuous wavelet transform (WT) of at is expressed as:
Further,
The local Hölder exponent of strength of singularity can be evaluated as the scaling power of the wavelet coefficient at for [19].
3. Engine health analysis
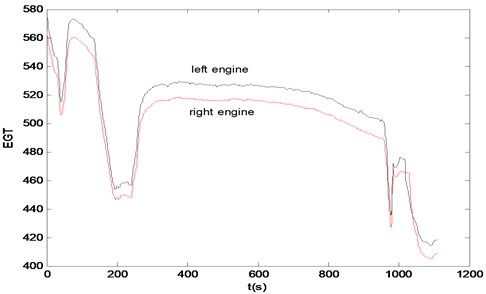
The effectiveness of the proposed technique in perceiving the fracture failure will be discussed in this section. The exhaust gas temperature (EGT), offered by a Commercial Company in Beijing, are applied. Specifically, we consider time series of two plane, aircraft A and aircraft B, in this paper. Fig. 1 shows a section of the normal EGT data from aircraft A.
Fig. 1The EGT data for normal engine of left and right in aircraft A
3.1. Example 1: Aircraft A
In order to test the robustness of the proposed fractal comparative diagnostics method, cruise mode time series of aircraft A are used in this section.
Fig. 2The Hölder exponents of (a) left engine and (b) right engine
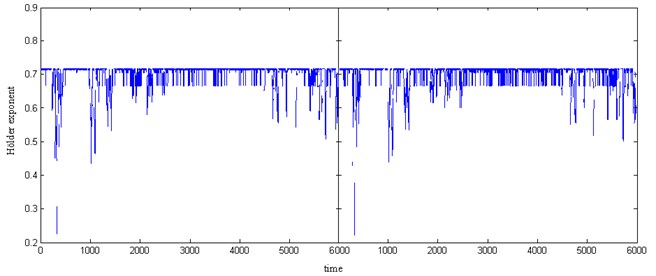
Here, we apply the Hölder exponent analysis method to signal of left and right engine for aircraft A, see Fig. 2, where one of the engine is fracture failure. We observe that there are different scaling phenomena in the plot. And then, we can study the difference between the Hölder exponents of left and right engine by using error function. The error function is defined as:
where are these Hölder exponents of left engine, are Hölder exponents of right engine respectively.
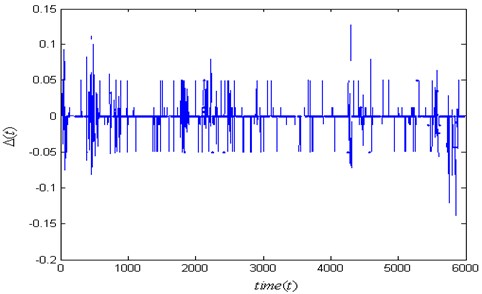
Fig. 3 shows the nontrivial difference between the Hölder exponents of left and right engine where one of the two engines is fracture failure. And then, we calculate the Hölder exponents for are normal engine as shown in Fig. 4.
Fig. 5 indicates the error function for Hölder exponents in normal engine , where , and are the Hölder exponent of normal left and right engine. Approximate to 0, compare to the nontrivial difference in Fig. 3.
Fig. 3The error function Δf(t) for one of the two engines is fracture failure in aircraft A
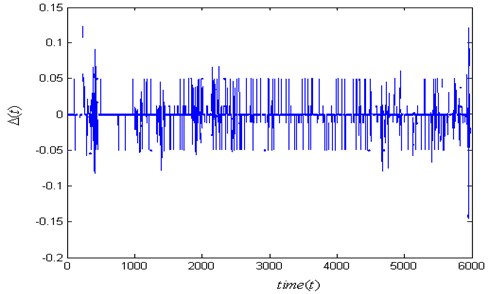
Fig. 4The Hölder exponents of normal engine (a) left and (b) right for aircraft A
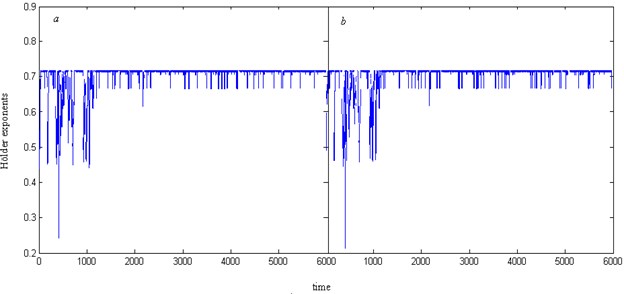
Fig. 5The error function Δn(t) of normal left and right engine for aircraft A. Δf(t)>>Δn(t) indicate the Hölder exponent method to diagnose engine fault is available
3.2. Example 2: Aircraft B
To examine the availability of fractal comparative diagnostics method using data in aircraft B, we apply the Hölder exponent analysis method again.
Here, the Hölder exponent are calculated for aircraft B, as show in Fig. 6, where one of the engine is fracture failure. Obviously, there are different scaling phenomena between the Hölder exponents of left and right engine. For analysing the dissimilarity, the error function defined by Eq. (4) is employed once again.
Fig. 6The Hölder exponents of (a) left engine and (b) right engine for aircraft B where one of the engine is fracture failure
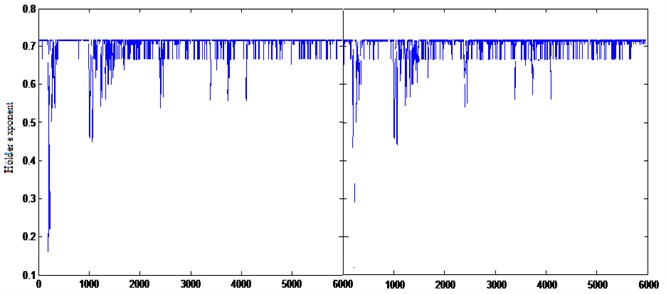
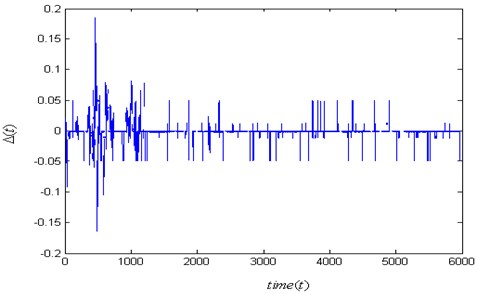
Fig. 7The error function Δf(t) for one of the two engines is fracture failure in aircraft B
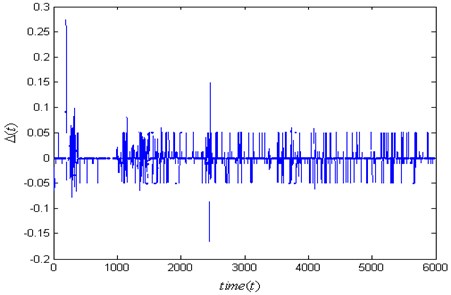
Fig. 8The Hölder exponents of (a) left engine and (b) right engine for aircraft B for normal engine
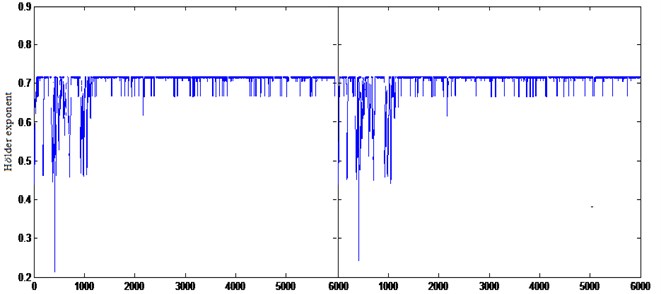
We represent the error function between the Hölder exponents of left and right engine in Fig. 7. For comparison, we calculate the Hölder exponents for are normal engine as shown in Fig. 8.
In Fig. 7, we observe that the nontrivial values of error function , where one of the engines is fracture failure. For comparison, the error function:
for normal engine are shown in Fig. 9. As expected the error function is less than the error function distinctly. We show the negligible difference between the Hölder exponents of left and right engine in Fig. 9, where both the left and right engine are normal.
Fig. 9The error function Δn(t) of normal left and right engine for aircraft B. The error function Δf(t)>>Δn(t) indicate the Hölder exponent method is available for diagnosing engine fault
4. Conclusions
We present a method of estimating the engine health and performance. The method is motivated by the local Hölder exponent theory, and implemented on the comparative analysis. Contrary to the intrinsically time-frequency analysis, this estimate is robust by providing stable, effective Hölder exponents, local in scale and position.
In this paper, we consider the effectiveness of the proposed method by applying it to time series collected at different aircraft. The conclusions indicate that the difference between left and right engine is obvious when one of the engines is fracture failure. On the other hand, the difference between the local Hölder exponents of left and right engine is trivial while two engines are normal. Therefore, we do believe that our monitoring algorithm may provide some help to analyze the aeroengine health and performance.
References
-
Trujillo L., Legrand P., Olague G., Lévy-Véhel J. Evolving estimators of the pointwise Hölder exponent with genetic programming. Information Sciences, Vol. 209, 2012, p. 61-79.
-
Jade A. M., Jayaraman V. K., Kulkarni B. D., Khopkar A. R., Ranade V. V., Sharma A. A novel local singularity distribution based method for flow regime identification: Gas–liquid stirred vessel with Rushton turbine. Chemical Engineering Science, Vol. 61, Issue 2, 2006, p. 688-697.
-
Hambaba A., Huff A. E. Multiresolution error detection on early fatigue cracks in gears. IEEE Aerospace Conference Proceedings, 2000.
-
Peng Z., He Y., Chen Z., Chu F. Identification of the shaft orbit for rotating machines using wavelet modulus. Mechanical Systems and Signal Processing, 2002.
-
Ruan Y., Zhou W. Long-term correlations and multifractal nature in the intertrade durations of a liquid Chinese stock and its warrant. Physica A, Vol. 390, Issue 9, 2011, p. 1646-1654.
-
Aspenberg M., Graczyk J. Dimension and measure for semi-hyperbolic rational maps of degree 2 dimension at mesure pour les applications rationnelles semi-hyperboliques de degré 2. Comptes Rendus Mathematique, Vol. 347, Issue 7-8, 2009, p. 395-400.
-
Robertson A. N., Farrar C. R., Sohn H. Singularity detection for structural health monitoring using Hölder exponents. Mechanical Systems and Signal Processing, Vol. 17, Issue 6, 2003, p. 1163-1184.
-
Arneodo A., Bacry E., Muzy J. F. Wavelets and multifractal formalism for singular signals: application to turbulence data. PRL, Vol. 67, Issue 25, 1991, p. 3515-3518.
-
Arneodo A., Bacry E., Muzy J. F. The thermodynamics of fractals revisited with wavelets. Physica A, Vol. 213, 1995, p. 232-275.
-
West B. J., Scafetta N., Cooke W. H., Balocchi R. Influence of progressive central hypovolemia on hölder exponent distributions of cardiac interbeat intervals. Ann. Biomed. Eng., Vol. 32, 2004, p. 1077-1087.
-
Bianchi S., Pianese A. Multifractional properties of stock indices decomposed by filtering their pointwise Hölder regularity. International Journal of Theoretical and Applied Finance, Vol. 11, 2008, p. 567-595.
-
Bianchi S., Pantanella A. Pointwise regularity exponents and market cross-correlation. International Review of Business Research Papers, Vol. 1, 2010, p. 39-51.
-
Nakamura T., Horio H., Chiba Y. Local Hölder exponent analysis of heart rate variability in preterm infants. IEEE Transactions on biomedical engineering, Vol. 53, 2006, p. 83-88.
-
Ivanov P. C., Amaral L. A., Goldberger A. L., Havlin S., Rosenblum M. G., Struzik Z. R., Stanley H. E. Multifractality in human heartbeat dynamics. Nature, Vol. 399, 1999, p. 461-465.
-
Muzy J. F., Bacry E., Arneodo A. The multifractal formalism revisited with wavelets. Int. J. Bif. Chaos, Vol. 4, 1994, p. 245-302.
-
Jaw L. C. Recent advancements in aircraft engine health management (EHM) technologies and recommendations for the next step. 50th ASME International Gas Turbine & Aeroengine Technical Congress, Nevada, 2005.
-
Dalpiaz G., Rivola A., Rubini R. Effectiveness and sensitivity of vibration processing techniques for local fault detection in gears. Mechanical Systems and Signal Processing, Vol. 14, Issue 3, 2000, p. 387-412.
-
Jaffard S. Multifractal formalism for functions: I. Results valid for all functions, II. Self-similar functions. SIAM J. Math. Anal., Vol. 28, 1997, p. 944-998.
-
Mallat S. G., Hwang W. L. Singularity detection and processing with wavelets. IEEE Trans. Inf. Theory, Vol. 38, 1992, p. 617-643.
About this article
The financial support from the funds of the Fundamental Research Funds for the Central Universities under Grant No. ZXH2012C002, the National Natural Science Foundation of China under Grant No. U1233201, and Natural Science Foundation of Hebei Province (E2012402013) are gratefully acknowledged.
